题目内容
6．
如图，AB，CD是⊙O的两条弦，连接AD，BC，若∠BCD=50°，则∠BAD的度数为（ ）| A． | 70° | B． | 60° | C． | 50° | D． | 40° |
分析 直接根据圆周角定理求解．
解答 解：∵∠BCD=70°，
∴∠BAD=∠BCD=70°．
故选C．
点评 本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
相关题目
16．
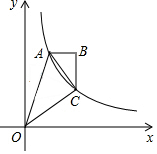如图，双曲线y=$\frac{2}{x}$（x＞0）经过四边形OABC的顶点A、C，∠ABC=90°，AC平分∠OAB，OC平分OA与x轴正半轴的夹角，AB∥x轴，则△OAC的面积是（ ）
如图，双曲线y=$\frac{2}{x}$（x＞0）经过四边形OABC的顶点A、C，∠ABC=90°，AC平分∠OAB，OC平分OA与x轴正半轴的夹角，AB∥x轴，则△OAC的面积是（ ）| A． | 1.5 | B． | 1.6 | C． | 1.8 | D． | 2 |
17．
雷达二维平面定位的主要原理是：测量目标的两个信息--距离和角度，目标的表示方法为（γ，α），其中，γ表示目标与探测器的距离；α表示以正东为始边，逆时针旋转后的角度．如图，雷达探测器显示在点A，B，C处有目标出现，其中，目标A的位置表示为A（5，30°），目标B的位置表示为F（4，150°）．用这种方法表示目标C的位置，正确的是（ ）
雷达二维平面定位的主要原理是：测量目标的两个信息--距离和角度，目标的表示方法为（γ，α），其中，γ表示目标与探测器的距离；α表示以正东为始边，逆时针旋转后的角度．如图，雷达探测器显示在点A，B，C处有目标出现，其中，目标A的位置表示为A（5，30°），目标B的位置表示为F（4，150°）．用这种方法表示目标C的位置，正确的是（ ）| A． | （-3，300°） | B． | （3，60°） | C． | （3，300°） | D． | （-3，60°） |
14．
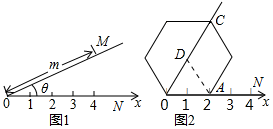阅读理解：如图①所示，在平面内选一定点O，引一条有方向的射线ON，再选定一个单位长度，那么平面上任一点M的位置可由OM的长度m与∠MON的度数θ确定，有序数对（m，θ）称为M点的“极坐标”，这样建立的坐标系称为“极坐标系”．
应用：在图②的极坐标系下，如果正六边形的边长为2，有一边OA在射线ON上，则正六边形的顶点C的极坐标应记为（ ）
阅读理解：如图①所示，在平面内选一定点O，引一条有方向的射线ON，再选定一个单位长度，那么平面上任一点M的位置可由OM的长度m与∠MON的度数θ确定，有序数对（m，θ）称为M点的“极坐标”，这样建立的坐标系称为“极坐标系”．应用：在图②的极坐标系下，如果正六边形的边长为2，有一边OA在射线ON上，则正六边形的顶点C的极坐标应记为（ ）
| A． | （4，60°） | B． | （4，45°） | C． | （2$\sqrt{2}$，60°） | D． | （2$\sqrt{2}$，50°） |
18．将直线y=2x+3向下平移4个单位长度，得到的直线的函数表达式是（ ）
| A． | y=2x-1 | B． | y=2x+1 | C． | y=-4x+3 | D． | y=2x+7 |
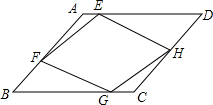如图，E、F、G、H分别为?ABCD的边AD、AB、BC、CD上的点，且AE=CG，BF=DH．求证：四边形EFGH是平行四边形．