题目内容
19.化简:$\frac{2{x}^{2}-2x}{{x}^{2}-1}$-$\frac{x-1}{x+1}$=1.分析 先通分,把分母不相同的几个分式化成分母相同的分式,经过通分,异分母分式的加减就转化为同分母分式的加减.
解答 解:$\frac{2{x}^{2}-2x}{{x}^{2}-1}$-$\frac{x-1}{x+1}$
=$\frac{2x(x-1)}{(x+1)(x-1)}$-$\frac{x-1}{x+1}$
=$\frac{2x}{x+1}$-$\frac{x-1}{x+1}$
=$\frac{2x-x+1}{x+1}$
=$\frac{x+1}{x+1}$
=1.
故答案为:1.
点评 本题主要考查了分式的加减法,解题时注意:分式的通分必须注意整个分子和整个分母,分母是多项式时,必须先分解因式,分子是多项式时,要把分母所乘的相同式子与这个多项式相乘,而不能只同其中某一项相乘.

练习册系列答案
相关题目
14.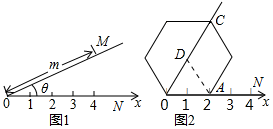 阅读理解:如图①所示,在平面内选一定点O,引一条有方向的射线ON,再选定一个单位长度,那么平面上任一点M的位置可由OM的长度m与∠MON的度数θ确定,有序数对(m,θ)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
阅读理解:如图①所示,在平面内选一定点O,引一条有方向的射线ON,再选定一个单位长度,那么平面上任一点M的位置可由OM的长度m与∠MON的度数θ确定,有序数对(m,θ)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图②的极坐标系下,如果正六边形的边长为2,有一边OA在射线ON上,则正六边形的顶点C的极坐标应记为( )
 阅读理解:如图①所示,在平面内选一定点O,引一条有方向的射线ON,再选定一个单位长度,那么平面上任一点M的位置可由OM的长度m与∠MON的度数θ确定,有序数对(m,θ)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
阅读理解:如图①所示,在平面内选一定点O,引一条有方向的射线ON,再选定一个单位长度,那么平面上任一点M的位置可由OM的长度m与∠MON的度数θ确定,有序数对(m,θ)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.应用:在图②的极坐标系下,如果正六边形的边长为2,有一边OA在射线ON上,则正六边形的顶点C的极坐标应记为( )
| A. | (4,60°) | B. | (4,45°) | C. | (2$\sqrt{2}$,60°) | D. | (2$\sqrt{2}$,50°) |
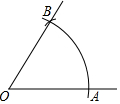 如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则可判定△AOB为等边三角形的依据是三边相等的三角形为等边三角形.
如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则可判定△AOB为等边三角形的依据是三边相等的三角形为等边三角形.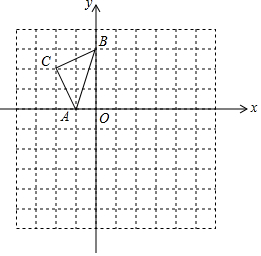 如图,在已知的平面直角坐标系中,△ABC的顶点都在正方形网格的格点上,若A,B两点的坐标分别是A(-1,0),B(0,3).
如图,在已知的平面直角坐标系中,△ABC的顶点都在正方形网格的格点上,若A,B两点的坐标分别是A(-1,0),B(0,3).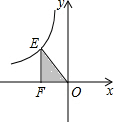 位于第二象限的点E在反比例函数y=$\frac{k}{x}$的图象上,点F在x轴的负半轴上,O是坐标原点,若FO⊥EF,△EOF的面积等于2,则k的值是( )
位于第二象限的点E在反比例函数y=$\frac{k}{x}$的图象上,点F在x轴的负半轴上,O是坐标原点,若FO⊥EF,△EOF的面积等于2,则k的值是( )
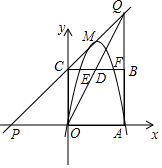 如图,抛物线y=-x2+2mx(m>1)交x轴于点O,A,顶点为M,以OA为边向上方作正方形OABC,直线CM交x轴于点P,交直线AB于点Q,连接OQ交直线BC于点D,
如图,抛物线y=-x2+2mx(m>1)交x轴于点O,A,顶点为M,以OA为边向上方作正方形OABC,直线CM交x轴于点P,交直线AB于点Q,连接OQ交直线BC于点D, 如图,小明在大楼45米高(即PH=45米)的窗户P处进行观测,测得山坡上A处的俯角为15°,山脚B处得俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$.点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上且PH⊥HC,求A、B两点间的距离(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.732.
如图,小明在大楼45米高(即PH=45米)的窗户P处进行观测,测得山坡上A处的俯角为15°,山脚B处得俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$.点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上且PH⊥HC,求A、B两点间的距离(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.732.