题目内容
4.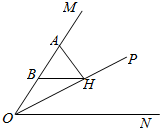 如图,OP平分∠MON,AH⊥OP于H,B是AO的中点,求证:BH∥ON.
如图,OP平分∠MON,AH⊥OP于H,B是AO的中点,求证:BH∥ON.
分析 根据直角三角形的性质得到BH=$\frac{1}{2}$OA=OB,根据等腰三角形的性质得到∠BOH=∠BHO,根据角平分线的定义、平行线的判定定理证明.
解答 证明:∵AH⊥OP,B是AO的中点,
∴BH=$\frac{1}{2}$OA=OB,
∴∠BOH=∠BHO,
∵OP平分∠MON,
∴∠BOH=∠NOP,
∴∠BHO=∠NOP,
∴BH∥ON.
点评 本题考查的是直角三角形的性质、角平分线的定义,掌握直角三角形中,斜边上的中线等于斜边的一半是解题的关键.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
7.一组数据2,4,5,2,3的众数和中位数分别是( )
| A. | 2,5 | B. | 2,2 | C. | 2,3 | D. | 3,2 |
16.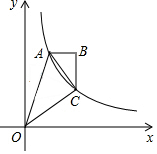 如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,AC平分∠OAB,OC平分OA与x轴正半轴的夹角,AB∥x轴,则△OAC的面积是( )
如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,AC平分∠OAB,OC平分OA与x轴正半轴的夹角,AB∥x轴,则△OAC的面积是( )
 如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,AC平分∠OAB,OC平分OA与x轴正半轴的夹角,AB∥x轴,则△OAC的面积是( )
如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,AC平分∠OAB,OC平分OA与x轴正半轴的夹角,AB∥x轴,则△OAC的面积是( )| A. | 1.5 | B. | 1.6 | C. | 1.8 | D. | 2 |
14.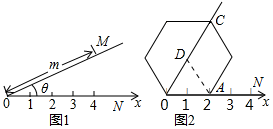 阅读理解:如图①所示,在平面内选一定点O,引一条有方向的射线ON,再选定一个单位长度,那么平面上任一点M的位置可由OM的长度m与∠MON的度数θ确定,有序数对(m,θ)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
阅读理解:如图①所示,在平面内选一定点O,引一条有方向的射线ON,再选定一个单位长度,那么平面上任一点M的位置可由OM的长度m与∠MON的度数θ确定,有序数对(m,θ)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图②的极坐标系下,如果正六边形的边长为2,有一边OA在射线ON上,则正六边形的顶点C的极坐标应记为( )
 阅读理解:如图①所示,在平面内选一定点O,引一条有方向的射线ON,再选定一个单位长度,那么平面上任一点M的位置可由OM的长度m与∠MON的度数θ确定,有序数对(m,θ)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
阅读理解:如图①所示,在平面内选一定点O,引一条有方向的射线ON,再选定一个单位长度,那么平面上任一点M的位置可由OM的长度m与∠MON的度数θ确定,有序数对(m,θ)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.应用:在图②的极坐标系下,如果正六边形的边长为2,有一边OA在射线ON上,则正六边形的顶点C的极坐标应记为( )
| A. | (4,60°) | B. | (4,45°) | C. | (2$\sqrt{2}$,60°) | D. | (2$\sqrt{2}$,50°) |
 如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:
如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:
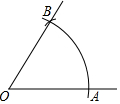 如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则可判定△AOB为等边三角形的依据是三边相等的三角形为等边三角形.
如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则可判定△AOB为等边三角形的依据是三边相等的三角形为等边三角形.