题目内容
11.某工厂生产A、B两种产品共50件,其生产成本与利润如下表.| A种产品 | B种产品 | |
| 成本(万元/件) | 1.2 | 1.8 |
| 利润(万元/件) | 0.4 | 0.8 |
分析 设生产A产品x件,则生产B产品(50-x)件,依据投入资金不超过80万元,且希望获利超过32万元,可得出不等式组,解出即可得出答案.
解答 解:设生产A产品x件,则生产B产品(50-x)件,
由题意得,投入资金不超过80万元,且希望获利超过32万元,
故可得:$\left\{\begin{array}{l}{1.2x+1.8(50-x)≤80}\\{0.4x+0.8(50-x)>32}\end{array}\right.$,
解得:$\frac{50}{3}$≤x<20,
∵x取整数,
∴x可取17、18、19,
共三种方案:①A 17件,B 33件;
②A 18件,B 32件;
③A 19件,B 31件.
第一种方案获利:0.4×17+0.8×33=33.2万元;
第二种方案获利:0.4×18+0.8×32=32.8万元;
第三种方案获利:0.4×19+0.8×31=32.4万元;
故可得方案一获利最大,最大利润为33.2万元.
答:工厂有3种生产方案,第一种方案获利润最大,最大利润是33.2万元.
点评 此题考查了一元一次不等式组的应用,属于实际应用类题目,解答本题的关键是根据题意不等关系得出不等式组,难度一般.

练习册系列答案
相关题目
2.根据下表中一次函数的自变量x和函数y的对应值,m的值为3.
| x | -1 | 0 | 1 |
| y | 7 | 5 | m |
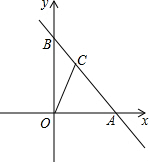 如图,直线y=-x+4与x轴交于点A,与y轴交于点B,点C在AB上,AC=2BC.求点C的坐标.
如图,直线y=-x+4与x轴交于点A,与y轴交于点B,点C在AB上,AC=2BC.求点C的坐标. 如图,直线y=-2x-4与坐标轴交于A、B两点,点P为直线y=2x上一点,且△ABP的面积被y轴分成1:2的两部分,求点P的坐标.
如图,直线y=-2x-4与坐标轴交于A、B两点,点P为直线y=2x上一点,且△ABP的面积被y轴分成1:2的两部分,求点P的坐标.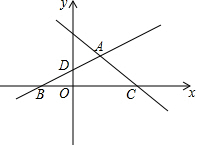 如图,在平面直角坐标系xOy中,直线y=-x+3与x轴交于点C,与y轴交于点E.与直线AD交于点A($\frac{4}{3}$,$\frac{5}{3}$),点D的坐标为(0,1).直线AD与x轴交于点B.
如图,在平面直角坐标系xOy中,直线y=-x+3与x轴交于点C,与y轴交于点E.与直线AD交于点A($\frac{4}{3}$,$\frac{5}{3}$),点D的坐标为(0,1).直线AD与x轴交于点B. 已知一次函数y=kx+b的图象经过点A(1,3)和B(-1,-1)两点.
已知一次函数y=kx+b的图象经过点A(1,3)和B(-1,-1)两点.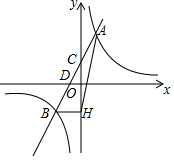 一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH.
一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH.