题目内容
16.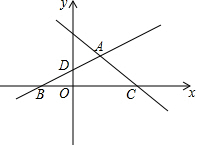 如图,在平面直角坐标系xOy中,直线y=-x+3与x轴交于点C,与y轴交于点E.与直线AD交于点A($\frac{4}{3}$,$\frac{5}{3}$),点D的坐标为(0,1).直线AD与x轴交于点B.
如图,在平面直角坐标系xOy中,直线y=-x+3与x轴交于点C,与y轴交于点E.与直线AD交于点A($\frac{4}{3}$,$\frac{5}{3}$),点D的坐标为(0,1).直线AD与x轴交于点B.(1)求直线AD的解析式;
(2)求∠ACO的度数;
(3)求△ABC的面积;
(4)求AB的长.
分析 (1)设直线AD的解析式为y=kx+b,用待定系数法将A($\frac{4}{3}$,$\frac{5}{3}$),D(0,1)的坐标代入即可;
(2)根据直线y=-x+3与x轴交于点C,与y轴交于点E,得到OC=OE=3,即△COE是等腰直角三角形,据此可得∠ACO的度数;
(3)先求得BC=5,再根据三角形面积计算公式进行计算即可;
(4)根据A($\frac{4}{3}$,$\frac{5}{3}$),B(-2,0),运用两点间距离公式进行计算即可.
解答 解:(1)设直线AD的解析式为y=kx+b,
将A($\frac{4}{3}$,$\frac{5}{3}$),D(0,1)代入得:
$\left\{\begin{array}{l}{\frac{4}{3}k+b=\frac{5}{3}}\\{1=b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=1}\end{array}\right.$.
故直线AD的解析式为:y=$\frac{1}{2}$x+1;
(2)∵直线y=-x+3与x轴交于点C,与y轴交于点E,
∴当x=0时,y=3;当y=0时,x=3,
∴C(3,0),E(0,3),
∴OC=OE=3,
即△COE是等腰直角三角形,
∴∠ACO=45°;
(3)∵直线AD的解析式为:y=$\frac{1}{2}$x+1,
∴当y=0时,x=-2,即B(-2,0),
∴BC=5,
∴△ABC的面积=$\frac{1}{2}$×5×$\frac{5}{3}$=$\frac{25}{6}$;
(4)根据两点间距离公式可得,
AB=$\sqrt{(\frac{4}{3}+2)^{2}+(\frac{5}{3})^{2}}$=$\frac{5}{3}\sqrt{5}$.
点评 本题主要考查了两直线相交问题,待定系数法求一次函数解析式的运用,解题时注意:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解.

 智能训练练测考系列答案
智能训练练测考系列答案| A种产品 | B种产品 | |
| 成本(万元/件) | 1.2 | 1.8 |
| 利润(万元/件) | 0.4 | 0.8 |
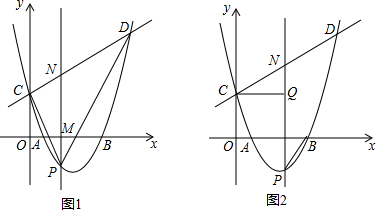
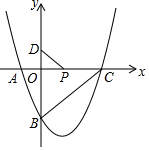 二次函数y=ax2-2x+c的图象与x轴交于A(-1,0),C(3,0),与y轴交于点B.
二次函数y=ax2-2x+c的图象与x轴交于A(-1,0),C(3,0),与y轴交于点B.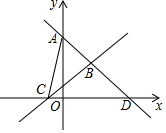 如图,直线y=$-\frac{4}{3}x+4$与y轴交于点A,与x轴交于点D,直线y=$\frac{4}{5}x+\frac{4}{5}$与x轴交于点C,且两直线相交于点B,求△ABC的面积.
如图,直线y=$-\frac{4}{3}x+4$与y轴交于点A,与x轴交于点D,直线y=$\frac{4}{5}x+\frac{4}{5}$与x轴交于点C,且两直线相交于点B,求△ABC的面积.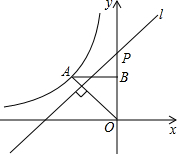 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A(-2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是1+$\sqrt{5}$.
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A(-2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是1+$\sqrt{5}$.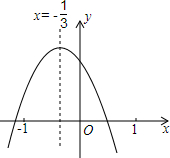 乐乐从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下列4条信息:
乐乐从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下列4条信息: