题目内容
19.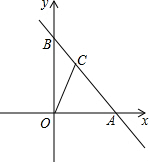 如图,直线y=-x+4与x轴交于点A,与y轴交于点B,点C在AB上,AC=2BC.求点C的坐标.
如图,直线y=-x+4与x轴交于点A,与y轴交于点B,点C在AB上,AC=2BC.求点C的坐标.
分析 先根据直线解析式求出A、B两点的坐标,再过点C作y轴的垂线,垂足为点D,则△CBD∽△ABO,运用相似三角形对应边成比例求出CD、BD的长,进而求出点C的坐标.
解答 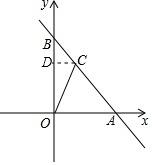 解:∵直线y=-x+4与x轴交于点A,与y轴交于点B,
解:∵直线y=-x+4与x轴交于点A,与y轴交于点B,
∴A(4,0),B(0,4),
∴OA=4,OB=4.
过点C作y轴的垂线,垂足为点D,则CD∥OA,
∴△CBD∽△ABO,
∴$\frac{CD}{OA}$=$\frac{BD}{OB}$=$\frac{BC}{AB}$,
∵AC=2BC,
∴$\frac{CD}{4}$=$\frac{BD}{4}$=$\frac{1}{3}$,
∴CD=BD=$\frac{4}{3}$,
∴OD=OB-BD=4-$\frac{4}{3}$=$\frac{8}{3}$.
∴C($\frac{4}{3}$,$\frac{8}{3}$).
点评 本题考查了一次函数图象上点的坐标特征,相似三角形的判定和性质,正确作出辅助线是解题的关键.

练习册系列答案
相关题目
2.2017的相反数是( )
| A. | -2017 | B. | 2017 | C. | -$\frac{1}{2017}$ | D. | $\frac{1}{2017}$ |
3.关于x的一元二次方程x2+3x+m=0有两个不相等的实数根,则m的取值范围为( )
| A. | m≤$\frac{9}{4}$ | B. | m$<\frac{9}{4}$ | C. | m≤$\frac{4}{9}$ | D. | m$<\frac{4}{9}$ |
11.某工厂生产A、B两种产品共50件,其生产成本与利润如下表.
若该工厂计划投人资金不超过80万元,且希望获利超过32万元,问该工厂有哪几种生产方案?哪种生产方案获得的利润最大?最大利润是多少?
| A种产品 | B种产品 | |
| 成本(万元/件) | 1.2 | 1.8 |
| 利润(万元/件) | 0.4 | 0.8 |
9.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
下列结论错误的是( )
| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
| A. | ac<0 | B. | 当x>1时,y的值随x的增大而减小 | ||
| C. | 3是方程ax2+(b-1)x+c=0的一个根 | D. | 当-1<x<3时,ax2+(b-1)x+c>0 |
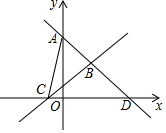 如图,直线y=$-\frac{4}{3}x+4$与y轴交于点A,与x轴交于点D,直线y=$\frac{4}{5}x+\frac{4}{5}$与x轴交于点C,且两直线相交于点B,求△ABC的面积.
如图,直线y=$-\frac{4}{3}x+4$与y轴交于点A,与x轴交于点D,直线y=$\frac{4}{5}x+\frac{4}{5}$与x轴交于点C,且两直线相交于点B,求△ABC的面积.