题目内容
3.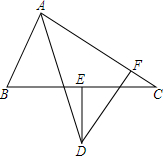 如图,AD平分∠BAC,与BC的垂直平分线交于点D,DF⊥AC于F.求证:AB+AC=2AF.
如图,AD平分∠BAC,与BC的垂直平分线交于点D,DF⊥AC于F.求证:AB+AC=2AF.
分析 根据线段垂直平分线求出BE=CE,根据角平分线性质求出EF=GE,证出Rt△BFE≌Rt△CGE,再判断出△AFE≌△AGE,推出AF=AG,即可.
解答 证明:
连接DB和CD,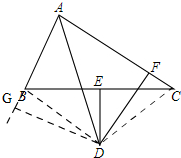 过点D作DG⊥AB,
过点D作DG⊥AB,
∵DE是BC的垂直平分线,
∴BD=CD,
∵AD平分∠BAC,DG⊥AB,DF⊥AC,
∴∠BGD=∠DGC=90°,DF=DG,
在Rt△BDG和Rt△CDF中$\left\{\begin{array}{l}{BD=CD}\\{DG=CD}\end{array}\right.$
∴Rt△BDG≌Rt△CDF(HL),
∴BG=CF;
∵AD平分∠BAC,DF⊥AB,DG⊥AC,
∴∠AFD=∠AGD=90°,∠FAD=∠GAD,
在△AFD和△AGD中$\left\{\begin{array}{l}{∠GAD=∠FAD}\\{∠AGD=∠AFD}\\{AD=AD}\end{array}\right.$
∴△AFD≌△AGD,
∴AF=AG,
∵BF=CG,
∴AB+AC=AF-BF+AG+CG=AF+AF=2AF,
∴AB+AC=2AF.
点评 本题考查了全等三角形的性质和判定,角平分线性质,线段垂直平分线性质的应用,能综合运用性质进行推理是解此题的关键,题目比较典型,难度适中.

练习册系列答案
相关题目
7.为了调查一个品种的草莓的产量,分别在4个大棚种植,获得的亩产是1100kg,1200kg,1100kg,1180kg.这组数据的众数和中位数分别是( )
| A. | 1100kg,1100kg | B. | 1100kg,1140kg | C. | 1140kg,1140kg | D. | 1100kg,1150kg |
4.函数y=$\frac{\sqrt{x+1}}{{x}^{2}-4}$的自变量x的取值范围是( )
| A. | x≥-1 | B. | x≥-1且x≠2 | C. | x≠±2 | D. | x>-1且x≠2 |
15.下列条件中不能判定两个直角三角形全等的是( )
| A. | 两个锐角分别对应相等 | B. | 两条直角边分别对应相等 | ||
| C. | 一条直角边和斜边分别对应相等 | D. | 一个锐角和一条斜边分别对应相等 |

 如图,已知直线y=x+3的图象与x,y的轴交于B,A两点,直线l经过A点,与线段OB交于点C且把△AOB面积分为2:1两部分.
如图,已知直线y=x+3的图象与x,y的轴交于B,A两点,直线l经过A点,与线段OB交于点C且把△AOB面积分为2:1两部分.