题目内容
12. 如图,已知直线y=x+3的图象与x,y的轴交于B,A两点,直线l经过A点,与线段OB交于点C且把△AOB面积分为2:1两部分.
如图,已知直线y=x+3的图象与x,y的轴交于B,A两点,直线l经过A点,与线段OB交于点C且把△AOB面积分为2:1两部分.(1)求线段OA,OB的长;
(2)求直线l的解析式.
分析 (1)先令x=0求出y的值,再令y=0求出x的值即可;
(2)根据△ABC与△AOC的高相等即可得出C点坐标,求出直线l的解析式即可.
解答 解:(1)∵令x=0,则y=3;令y=0,则x=-3,
∴A(0,3),B(-3,0);
(2)∵△ABC与△AOC的高相等,B(-3,0),线段OB交于点C且把△AOB面积分为2:1两部分,
∴C(-1,0)或(-2,0).
设直线l的解析式为y=kx+b(k≠0),
当C(-1,0)时,$\left\{\begin{array}{l}b=3\\-k+b=0\end{array}\right.$,解得$\left\{\begin{array}{l}b=3\\ k=3\end{array}\right.$;
当C(-2,0).时,$\left\{\begin{array}{l}b=3\\-2k+b=0\end{array}\right.$,解得$\left\{\begin{array}{l}b=3\\ k=\frac{3}{2}\end{array}\right.$.
故直线l的解析式为y=3x+3或y=$\frac{3}{2}$x+3.
点评 本题考查的是待定系数法求出一次函数的解析式,在解答(2)时要注意进行分类讨论.

练习册系列答案
相关题目
15.下列函数中,y是x的正比例函数的是( )
| A. | y=2x+1 | B. | $y=\frac{x}{3}$ | C. | y=2x2 | D. | $y=\frac{3}{x}$ |
7. 如图,将一张边长为4的正三角形纸片剪成四个全等的小正三角形,得到4个小正三角形,然后将其中的一个三角形再剪成四个全等的小正三角形,得到7个小正三角形.根据以上操作,若得到2017个小正三角形时,则最小正三角形的面积等于( )
如图,将一张边长为4的正三角形纸片剪成四个全等的小正三角形,得到4个小正三角形,然后将其中的一个三角形再剪成四个全等的小正三角形,得到7个小正三角形.根据以上操作,若得到2017个小正三角形时,则最小正三角形的面积等于( )
 如图,将一张边长为4的正三角形纸片剪成四个全等的小正三角形,得到4个小正三角形,然后将其中的一个三角形再剪成四个全等的小正三角形,得到7个小正三角形.根据以上操作,若得到2017个小正三角形时,则最小正三角形的面积等于( )
如图,将一张边长为4的正三角形纸片剪成四个全等的小正三角形,得到4个小正三角形,然后将其中的一个三角形再剪成四个全等的小正三角形,得到7个小正三角形.根据以上操作,若得到2017个小正三角形时,则最小正三角形的面积等于( )| A. | $\frac{\sqrt{3}}{{4}^{670}}$ | B. | ($\frac{1}{4}$)671$•\sqrt{3}$ | C. | $\frac{1}{{4}^{671}}$ | D. | $\frac{2\sqrt{3}}{{4}^{670}}$ |
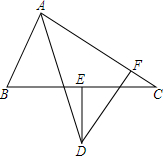 如图,AD平分∠BAC,与BC的垂直平分线交于点D,DF⊥AC于F.求证:AB+AC=2AF.
如图,AD平分∠BAC,与BC的垂直平分线交于点D,DF⊥AC于F.求证:AB+AC=2AF.

 如图,方格纸每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,点A(1,0),B(5,0),C(3,3),D(1,4).
如图,方格纸每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,点A(1,0),B(5,0),C(3,3),D(1,4).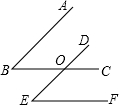 如图,已知BC、DE相交于点O,给出以下三个判断:①AB∥DE;②BC∥EF;③∠B=∠E,请你以其中两个判断作为条件,另外一个判断作为结论,写出所有的命题,指出这些命题是真命题还是假命题,并选择其中的一个真命题加以证明.
如图,已知BC、DE相交于点O,给出以下三个判断:①AB∥DE;②BC∥EF;③∠B=∠E,请你以其中两个判断作为条件,另外一个判断作为结论,写出所有的命题,指出这些命题是真命题还是假命题,并选择其中的一个真命题加以证明.