题目内容
13.(1)计算(π-$\sqrt{3}$)0+($\frac{1}{2}$)-1-$\sqrt{27}$(2)解不等式组$\left\{\begin{array}{l}{3y≥y+2}\\{4y-2<y+4}\end{array}\right.$.
分析 (2)用零指数,负整指数,二次根式的先化简,再合并即可;
(2)分别求解两个不等式的解集,最后确定出不等式组的解集.
解答 解:(1)原式=1+2-3$\sqrt{3}$=3-3$\sqrt{3}$
(2)$\left\{\begin{array}{l}{3y≥y+2①}\\{4y-2<y+4②}\end{array}\right.$
由①得y≥1
由②得y<2.
∴不等式租的解集为:1≤y<2.
点评 此题是解一元一次不等式,主要考查了幂的运算,二次根式的化简,不等式组解集的确定,解本题的关键熟练掌握实数的运算.

练习册系列答案
相关题目
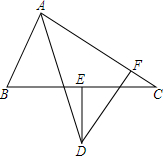 如图,AD平分∠BAC,与BC的垂直平分线交于点D,DF⊥AC于F.求证:AB+AC=2AF.
如图,AD平分∠BAC,与BC的垂直平分线交于点D,DF⊥AC于F.求证:AB+AC=2AF. 如图,方格纸每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,点A(1,0),B(5,0),C(3,3),D(1,4).
如图,方格纸每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,点A(1,0),B(5,0),C(3,3),D(1,4).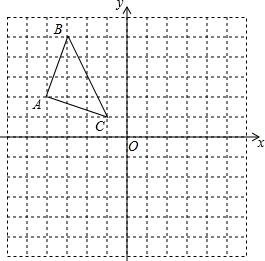 已知:如图,已知△ABC
已知:如图,已知△ABC 如图,△ABC中,D、E分别是AB、AC上的点,且满足AB•AD=AE•AC,连接DE
如图,△ABC中,D、E分别是AB、AC上的点,且满足AB•AD=AE•AC,连接DE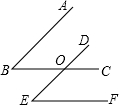 如图,已知BC、DE相交于点O,给出以下三个判断:①AB∥DE;②BC∥EF;③∠B=∠E,请你以其中两个判断作为条件,另外一个判断作为结论,写出所有的命题,指出这些命题是真命题还是假命题,并选择其中的一个真命题加以证明.
如图,已知BC、DE相交于点O,给出以下三个判断:①AB∥DE;②BC∥EF;③∠B=∠E,请你以其中两个判断作为条件,另外一个判断作为结论,写出所有的命题,指出这些命题是真命题还是假命题,并选择其中的一个真命题加以证明.