题目内容
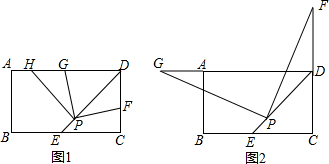
6.已知在矩形ABCD中,∠ADC的平分线DE与BC边所在的直线交于点E,点P是线段DE上一定点(其中EP<PD)(1)如图1,若点F在CD边上(不与D重合),将∠DPF绕点P逆时针旋转90°后,角的两边PD、PF分别交射线DA于点H、G.
①求证:PG=PF; ②探究:DF、DG、DP之间有怎样的数量关系,并证明你的结论.
(2)拓展:如图2,若点F在CD的延长线上(不与D重合),过点P作PG⊥PF,交射线DA于点G,你认为(1)中DF、DG、DP之间的数量关系是否仍然成立?若成立,给出证明;若不成立,请写出它们所满足的数量关系式,并说明理由.
分析 (1)①若证PG=PF,可证△HPG≌△DPF,已知∠DPH=∠HPG,由旋转可知∠GPF=∠HPD=90°及DE平分∠ADC得△HPD为等腰直角三角形,即∠DHP=∠PDF=45°、PD=PH,即可得证;
②由△HPD为等腰直角三角形,△HPG≌△DPF知HD=$\sqrt{2}$DP,HG=DF,根据DG+DF=DG+GH=DH即可得;
(2)过点P作PH⊥PD交射线DA于点H,先证△HPD为等腰直角三角形可得PH=PD,HD=$\sqrt{2}$DP,再证△HPG≌△DPF可得HG=DF,根据DH=DG-HG=DG-DF可得DG-DF=$\sqrt{2}$DP.
解答 解:(1)①∵∠GPF=∠HPD=90°,∠ADC=90°,
∴∠GPH=∠FPD,
∵DE平分∠ADC,
∴∠PDF=∠ADP=45°,
∴△HPD为等腰直角三角形,
∴∠DHP=∠PDF=45°,
在△HPG和△DPF中,
∵$\left\{\begin{array}{l}{∠PHG=∠PDF}\\{PH=PD}\\{∠GPH=∠FPD}\end{array}\right.$,
∴△HPG≌△DPF(ASA),
∴PG=PF;
②结论:DG+DF=$\sqrt{2}$DP,
由①知,△HPD为等腰直角三角形,△HPG≌△DPF,
∴HD=$\sqrt{2}$DP,HG=DF,
∴HD=HG+DG=DF+DG,
∴DG+DF=$\sqrt{2}$DP;
(2)不成立,数量关系式应为:DG-DF=$\sqrt{2}$DP,
如图,过点P作PH⊥PD交射线DA于点H,
∵PF⊥PG,
∴∠GPF=∠HPD=90°,
∴∠GPH=∠FPD,
∵DE平分∠ADC,且在矩形ABCD中,∠ADC=90°,
∴∠HDP=∠EDC=45°,得到△HPD为等腰直角三角形,
∴∠DHP=∠EDC=45°,且PH=PD,HD=$\sqrt{2}$DP,
∴∠GHP=∠FDP=180°-45°=135°,
在△HPG和△DPF中,
∵$\left\{\begin{array}{l}{∠GPH=∠FPD}\\{∠GHP=∠FDP}\\{PH=PD}\end{array}\right.$
∴△HPG≌△DPF,
∴HG=DF,
∴DH=DG-HG=DG-DF,
∴DG-DF=$\sqrt{2}$DP.
点评 本题主要考查等腰直角三角形的性质、全等三角形的判定与性质、矩形的性质的综合运用,灵活运用全等三角形的判定与性质将待求证线段关系转移至其他两线段间关系是解题的关键.

 如图,已知△ABC,AB=AC,∠A=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E、F.给出以下四个结论:
如图,已知△ABC,AB=AC,∠A=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E、F.给出以下四个结论:①AE=CF;
②EF=AP;
③△EPF是等腰直角三角形;
④S四边形AEPF=$\frac{1}{2}$S△ABC
上述结论始终正确的有( )
| A. | ①②③ | B. | ①③ | C. | ①③④ | D. | ①②③④ |
| A. | m-2>n-2 | B. | $\frac{m}{2}$>$\frac{n}{2}$ | C. | m2>n2 | D. | 2m+1>2n+1 |
| A. | y1=y2 | B. | y1>y2 | C. | y1<y2 | D. | 无法确定 |
| A. | 1.0703×1015立方米 | B. | 1.0703×1016立方米 | ||
| C. | 1.0703×1017立方米 | D. | 1.0703×1018立方米 |
| A. | y=2x+1 | B. | $y=\frac{x}{3}$ | C. | y=2x2 | D. | $y=\frac{3}{x}$ |
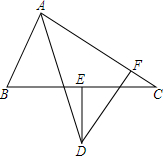 如图,AD平分∠BAC,与BC的垂直平分线交于点D,DF⊥AC于F.求证:AB+AC=2AF.
如图,AD平分∠BAC,与BC的垂直平分线交于点D,DF⊥AC于F.求证:AB+AC=2AF.