题目内容
8.已知:二次函数y=(a-3)x2-2(a2-6a+10)x+1(a≠3).(1)当a=5,求此二次函数图象的顶点坐标.
(2)设a为大于4的整数,x为正整数
①在括号内填上适当的内容使等式成立
由题意得抛物线的对称轴
h=$\frac{-2({a}^{2}-6a+10)}{2(a-3)}$=$\frac{{a}^{2}-6a+10}{()}$=$\frac{()^{2}+1}{a-3}$=a-3+$\frac{()}{a-3}$
②用a的代数式表示h的整数部分,并说明理由.
③当二次函数取得最小值时,求正整数x的值.(用a的代数式表示)
分析 (1)将a=5代入二次函数y=(a-3)x2-2(a2-6a+10)x+1,然后利用配方法求解即可求得此二次函数图象的顶点坐标.
(2)①首先根据公式求得对称轴,再化简,即可求得答案;②由①,即可求得答案;③分三种情形讨论即可.
解答 解:(1)当a=5时,二次函数y=(a-3)x2-2(a2-6a+10)x+1=2x2-10x+1=2(x-$\frac{5}{2}$)2-$\frac{23}{2}$;
∴此二次函数图象的顶点坐标为:($\frac{5}{2}$,-$\frac{23}{2}$);
(2)①h=-$\frac{-2({a}^{2}-6a+10)}{2(a-3)}$=$\frac{{a}^{2}-6a+10}{a-3}$=$\frac{(a-3)^{2}+1}{a-3}$=a-3+$\frac{1}{a-3}$,
故答案为:a-3,a-3,1;
②由①得:h的整数部分为:a-3;
理由:∵为大于4的整数,
∴a-3是大于1的整数,
∴$\frac{1}{a-3}$是小数,
∴h的整数部分为:a-3;
③当x=h=a-3+$\frac{1}{a-3}$时,二次函数取得最小值,
∵a为大于4的整数,x为正整数,
∴抛物线的开口向上,
∴x=a-3或a-2时取得最小值,
当x=a-3时,取得最小值,则有
a-3+$\frac{1}{a-3}$-(a-3)<(a-2)-a-3-$\frac{1}{a-3}$,解得a>5,
当x=a-3或a-2时取得最小值,则有a-3+$\frac{1}{a-3}$-(a-3)=(a-2)-a-3-$\frac{1}{a-3}$,解得a=5,此时x=2或3,
当x=a-2时取得最小值,则有a-3+$\frac{1}{a-3}$-(a-3)>(a-2)-a-3-$\frac{1}{a-3}$,解得a<5(不合题意)
综上所述,当a>5时,二次函数取得最小值时,x=a-2,
当a=5时,二次函数取得最小值时,x=2或3.
点评 此题属于二次函数的综合题.考查了二次函数的性质以及配方法的应用.注意掌握分类讨论思想的应用是解此题的关键.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案| A. | y1=y2 | B. | y1>y2 | C. | y1<y2 | D. | 无法确定 |
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
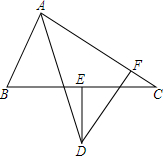 如图,AD平分∠BAC,与BC的垂直平分线交于点D,DF⊥AC于F.求证:AB+AC=2AF.
如图,AD平分∠BAC,与BC的垂直平分线交于点D,DF⊥AC于F.求证:AB+AC=2AF.
