题目内容
13.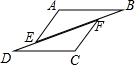 如图,已知B,F,E,D在同一条直线上,AB=CD,AB∥CD,BF=DE,求证:AE=CF.
如图,已知B,F,E,D在同一条直线上,AB=CD,AB∥CD,BF=DE,求证:AE=CF.
分析 利用SAS证明△ABE≌△CDF,根据全等三角形,对应边相等,可得到结论AE=CF.
解答 证明:∵BF=DE,
∴BE+EF=DE+EF.
即BE=DF,
∵AB∥CD,
∴∠B=∠D,
在△ABE和△CDF中,
$\left\{\begin{array}{l}{BE=DF}\\{∠B=∠D}\\{AB=CD}\end{array}\right.$,
∴△ABE≌△CDF.
∴AE=CF.
点评 本题考查了全等三角形的判定和性质;证明线段相等往往可以通过全等三角形来证明,这是一种经常用、很重要的方法,要注意掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.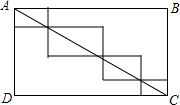 如图,在长方形ABCD中,AB=8,BC=5,则图中四个小长方形的周长和为( )
如图,在长方形ABCD中,AB=8,BC=5,则图中四个小长方形的周长和为( )
 如图,在长方形ABCD中,AB=8,BC=5,则图中四个小长方形的周长和为( )
如图,在长方形ABCD中,AB=8,BC=5,则图中四个小长方形的周长和为( )| A. | 13 | B. | 23 | C. | 24 | D. | 26 |
18. 如图,C点在线段AB上,点D是AC的中点,若CD=4cm,AB=13cm,则BC的长为( )
如图,C点在线段AB上,点D是AC的中点,若CD=4cm,AB=13cm,则BC的长为( )
 如图,C点在线段AB上,点D是AC的中点,若CD=4cm,AB=13cm,则BC的长为( )
如图,C点在线段AB上,点D是AC的中点,若CD=4cm,AB=13cm,则BC的长为( )| A. | 4cm | B. | 5cm | C. | 8cm | D. | 9cm |
 如图,抛物线y=-x2-2x+3与x轴交于A、B两点,与y轴交于点C,M为抛物线的顶点,点P为x轴负半轴上一点,PC交AM于E,若AE=CE,求点P的坐标.
如图,抛物线y=-x2-2x+3与x轴交于A、B两点,与y轴交于点C,M为抛物线的顶点,点P为x轴负半轴上一点,PC交AM于E,若AE=CE,求点P的坐标.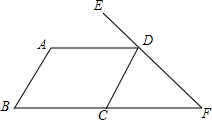 如图,∠A=120°,∠B=60°,∠EDA=55°,则∠F=55度.
如图,∠A=120°,∠B=60°,∠EDA=55°,则∠F=55度.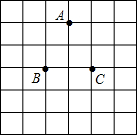 如图,在6×6的正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A,B,C都在格点上,在正方形网格中找到格点D,使以A,B,C,D为顶点的四边形是平行四边形,并画出所有符合要求的平行四边形.
如图,在6×6的正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A,B,C都在格点上,在正方形网格中找到格点D,使以A,B,C,D为顶点的四边形是平行四边形,并画出所有符合要求的平行四边形.