题目内容
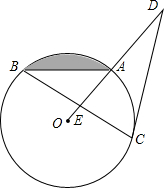 如图,在⊙O中,已知A是劣弧
如图,在⊙O中,已知A是劣弧 |
| BC |
(1)求∠ABC的度数;
(2)若AB=6,求图中弓形的面积.
考点:切线的性质,扇形面积的计算
专题:
分析:(1)连接OC,则∠OCD=90°,可求得∠DOC=60°,利用圆周角定理可求得∠ABC=
∠DOC=30°;
(2)由A为
的中点可知∠AOB=∠AOC=60°,可得△AOB为等边三角形,所以容易求得扇形AOB和△AOB的面积,从而可求得阴影部分的面积.
| 1 |
| 2 |
(2)由A为
 |
| BC |
解答:解:(1)如图1,连接OC,
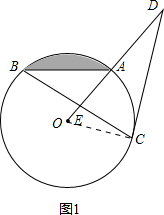
∵CD为⊙O的切线,
∴∠OCD=90°,且∠D=30°,
∴∠DOC=60°,
∴∠ABC=
∠DOC=30°;
(2)如图2,连接OB,

∵A为
的中点,
∴∠BOA=∠AOC=60°,
又∵OA=OB,
∴△AOB为等边三角形,
∴∠AOB=60°,OA=OB=AB=6,
∴S扇形AOB=
π•OA2=6π,S△AOB=
OA2=9
,
∴S阴影=S扇形AOB-S△AOB=6π-9
.

∵CD为⊙O的切线,
∴∠OCD=90°,且∠D=30°,
∴∠DOC=60°,
∴∠ABC=
| 1 |
| 2 |
(2)如图2,连接OB,

∵A为
 |
| BC |
∴∠BOA=∠AOC=60°,
又∵OA=OB,
∴△AOB为等边三角形,
∴∠AOB=60°,OA=OB=AB=6,
∴S扇形AOB=
| 1 |
| 6 |
| ||
| 4 |
| 3 |
∴S阴影=S扇形AOB-S△AOB=6π-9
| 3 |
点评:本题主要考查切线的性质及圆周角定理、扇形的有关计算,连接OC是解决切线问题的常用辅助线.求得∠AOB=60°是求阴影部分面积的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 的概率是0.5,即在一次试验中每个电子元件的状态有两个可能(通电、断开),并且这两个状态的可能行相等.
的概率是0.5,即在一次试验中每个电子元件的状态有两个可能(通电、断开),并且这两个状态的可能行相等.
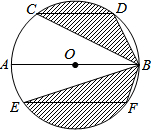 如图,AB是⊙O的直径,CD、EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8.则图中阴影部分的面积为
如图,AB是⊙O的直径,CD、EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8.则图中阴影部分的面积为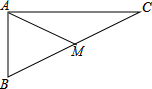 如图,在△ABC中,∠ABC=90°,AB=4cm,AC=6cm,AM是中线.
如图,在△ABC中,∠ABC=90°,AB=4cm,AC=6cm,AM是中线.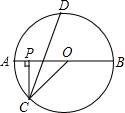 如图,P是⊙O的直径AB上的一点,PC⊥AB,PC交⊙O于C,∠OCP的平分线交⊙O于D,若点P在半径OA(不包括O点和A点)上移动时,试探究
如图,P是⊙O的直径AB上的一点,PC⊥AB,PC交⊙O于C,∠OCP的平分线交⊙O于D,若点P在半径OA(不包括O点和A点)上移动时,试探究