题目内容
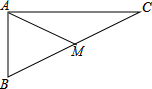 如图,在△ABC中,∠ABC=90°,AB=4cm,AC=6cm,AM是中线.
如图,在△ABC中,∠ABC=90°,AB=4cm,AC=6cm,AM是中线.(1)以A为圆心,4cm长为半径作⊙A,则点B、C、M与⊙A是什么位置关系?
(2)若以A为圆心作⊙A,使点B、C、M三点中至少有一点在圆内,且至少有一点在圆外,则⊙A的半径r的取值范围是什么?
考点:点与圆的位置关系
专题:
分析:(1)根据点与圆的位置关系判定方法,比较AB,AC,AM与AB的大小关系即可得出答案;
(2)利用分界点当B、C、M三点中至少有一点在⊙A内时,以及当至少有一点在⊙A外时,分别求出即可.
(2)利用分界点当B、C、M三点中至少有一点在⊙A内时,以及当至少有一点在⊙A外时,分别求出即可.
解答:解:(1)∵AB=4cm=⊙A的半径,
∴点B在⊙A上;
∵AC=6cm>4cm,
∴点C在⊙A外;
由勾股定理,得BC=
=2
cm,
∵AM是BC边上的中线,
∴AM=
BC=
cm<4cm,
∴点M在⊙A内;
(2)以点A为圆心作⊙A,使B、C、M三点中至少有一点在⊙A内时,r>
cm,
当至少有一点在⊙A外时,r<6cm,
故⊙A的半径r的取值范围为:
cm<r<6cm.
∴点B在⊙A上;
∵AC=6cm>4cm,
∴点C在⊙A外;
由勾股定理,得BC=
| AB2+AC2 |
| 13 |
∵AM是BC边上的中线,
∴AM=
| 1 |
| 2 |
| 13 |
∴点M在⊙A内;
(2)以点A为圆心作⊙A,使B、C、M三点中至少有一点在⊙A内时,r>
| 13 |
当至少有一点在⊙A外时,r<6cm,
故⊙A的半径r的取值范围为:
| 13 |
点评:此题主要考查了点与圆的位置关系:设⊙O的半径为r,点P到圆心的距离OP=d,则有:①点P在圆外?d>r;②点P在圆上?d=r;③点P在圆内?d<r.

练习册系列答案
相关题目
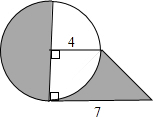 求阴影部分的面积:
求阴影部分的面积: 如图,在⊙O中,已知A是劣弧
如图,在⊙O中,已知A是劣弧
 如图,BC是⊙O的直径,A是圆上一点,AD⊥BC,垂足为点D.P为
如图,BC是⊙O的直径,A是圆上一点,AD⊥BC,垂足为点D.P为 如图所示,在等腰△ABC中,∠C=90°,AC=BC,BE=ED=CF,求∠CEF+∠CAD.
如图所示,在等腰△ABC中,∠C=90°,AC=BC,BE=ED=CF,求∠CEF+∠CAD.