题目内容
已知a-b=1,b-c=2,则a2+b2+c2-ab-bc-ac= .
考点:因式分解-运用公式法
专题:
分析:首先根据a-b=1,b-c=,2可得a-c=3,然后将原式因式分解后代入即可求解.
解答:解:∵a-b=1,b-c=2,
∴a-c=3,
∴a2+b2+c2-ab-bc-ac
=
(2a2+2b2+2c2-2ab-2bc-2ac)
=
[(a-b)2+(b-c)2+(c-a)2]
=7.
故答案为:7.
∴a-c=3,
∴a2+b2+c2-ab-bc-ac
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=7.
故答案为:7.
点评:本题考查了完全平方式.同学们能够运用完全平方式熟练推导与记忆a2+b2+c2-ab-bc-ac=
[(a-b)2+(b-c)2+(a-c)2]这是解题的关键.
| 1 |
| 2 |

练习册系列答案
相关题目
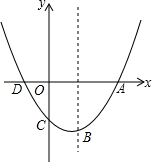 如图,已知抛物线y=
如图,已知抛物线y= 如图,□ABCD中,AE=EF=FB,BG=2CG,DE、DF分别交AG于点P,Q,则EP:PD=
如图,□ABCD中,AE=EF=FB,BG=2CG,DE、DF分别交AG于点P,Q,则EP:PD=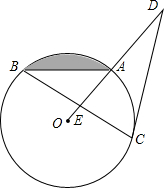 如图,在⊙O中,已知A是劣弧
如图,在⊙O中,已知A是劣弧