题目内容
16．已知点A（4，-3），B（x，-3），若AB∥x轴，且线段AB的长为5，x=-1或9．分析 由AB平行于x轴，A、B两点的纵坐标均为3，由线段AB的长为5，分点B在A的左、右两侧分别求之．
解答 解：∵AB平行于x轴，且A（4，-3），B（x，-3），线段AB的长为5，
∴点B的坐标为（-1，-3）或（9，-3）．
故x=-1或9．
故答案为：-1或9．
点评 本题主要考查坐标与图形性质，根据平行于x轴得出纵坐标相等是关键，要注意全面考虑到各种情况．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
6．
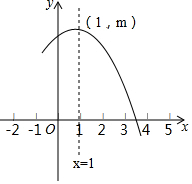如图是抛物线y=ax2+bx+c（a≠0）的部分图象，其顶点坐标为（1，m），且与x轴的一个交点在点（3，0）和（4，0）之间，下列结论错误的是（ ）
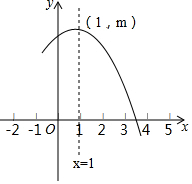如图是抛物线y=ax2+bx+c（a≠0）的部分图象，其顶点坐标为（1，m），且与x轴的一个交点在点（3，0）和（4，0）之间，下列结论错误的是（ ）| A． | a-b+c＞0 | |
| B． | b2=4a（c-m） | |
| C． | 2a+c＜0 | |
| D． | 一元二次方程ax2+bx+c=m-1有两个不相等的实数根 |
7．已知sinA=$\frac{1}{2}$，则∠A的度数为（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
11．下列四选项中，以三个实数为边长，能构成直角三角形的是（ ）
| A． | $\sqrt{3}$，2，$\sqrt{5}$ | B． | $\sqrt{1}$，$\sqrt{2}$，$\sqrt{3}$ | C． | $\sqrt{6}$，$\sqrt{8}$，$\sqrt{10}$ | D． | 3，4，6 |
5．
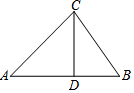如图，在△ABC中，CD⊥AB于点D，己知AC=a，∠A=α，∠B=β，则BD的长是（ ）
如图，在△ABC中，CD⊥AB于点D，己知AC=a，∠A=α，∠B=β，则BD的长是（ ）| A． | $\frac{a•sinα}{tanβ}$ | B． | $\frac{a•cosα}{tanβ}$ | C． | a•sinα•tanβ | D． | a•cosα•tanβ |