题目内容
11.下列四选项中,以三个实数为边长,能构成直角三角形的是( )| A. | $\sqrt{3}$,2,$\sqrt{5}$ | B. | $\sqrt{1}$,$\sqrt{2}$,$\sqrt{3}$ | C. | $\sqrt{6}$,$\sqrt{8}$,$\sqrt{10}$ | D. | 3,4,6 |
分析 欲求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可.
解答 解:A、($\sqrt{3}$)2+22≠($\sqrt{5}$)2,不能构成直角三角形;
B、($\sqrt{1}$)2+($\sqrt{2}$)2=($\sqrt{3}$)2,能构成直角三角形;
C、($\sqrt{6}$)2+($\sqrt{8}$)2≠($\sqrt{10}$)2,不能构成直角三角形;
D、32+42≠62,不能构成直角三角形.
故选B.
点评 本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.勾股定理的逆定理:若三角形三边满足a2+b2=c2,那么这个三角形是直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1. 如图,点C在以AB为直径的半圆O上(与点A,B不重合),则∠ACB( )
如图,点C在以AB为直径的半圆O上(与点A,B不重合),则∠ACB( )
 如图,点C在以AB为直径的半圆O上(与点A,B不重合),则∠ACB( )
如图,点C在以AB为直径的半圆O上(与点A,B不重合),则∠ACB( )| A. | 是锐角 | B. | 是直角 | C. | 是钝角 | D. | 大小不能确定 |
19.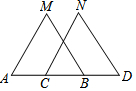 如图,在△ABM和△CDN中,A,C,B,D在同一条直线上,MB=ND,MA=NC,则下列条件中能判定△ABM≌△CDN的是( )
如图,在△ABM和△CDN中,A,C,B,D在同一条直线上,MB=ND,MA=NC,则下列条件中能判定△ABM≌△CDN的是( )
 如图,在△ABM和△CDN中,A,C,B,D在同一条直线上,MB=ND,MA=NC,则下列条件中能判定△ABM≌△CDN的是( )
如图,在△ABM和△CDN中,A,C,B,D在同一条直线上,MB=ND,MA=NC,则下列条件中能判定△ABM≌△CDN的是( )| A. | ∠MAB=∠NCD | B. | ∠MBA=∠NDC | C. | AC=BD | D. | AM∥CN |
6.下列哪些事件是必然事件( )
| A. | 5月1日前一天是4月30日 | B. | 一匹马的奔跑速度是70米/秒 | ||
| C. | 射击运动员一次命中10环 | D. | 明年元旦是晴天 |
 小猫在如图所示的地面上自由地走来走去,并随意停留在某块方砖上(图中每一块方砖除颜色外完全相同),小猫的大小忽略不计,则小猫停留在白色方砖上的概率是$\frac{5}{8}$.
小猫在如图所示的地面上自由地走来走去,并随意停留在某块方砖上(图中每一块方砖除颜色外完全相同),小猫的大小忽略不计,则小猫停留在白色方砖上的概率是$\frac{5}{8}$. 如图,在?ABCD中,P,Q分别是AD,BC的中点,求证:AC与PQ互相平分.
如图,在?ABCD中,P,Q分别是AD,BC的中点,求证:AC与PQ互相平分.