题目内容
1.图1是一个几何探究工具,其中△ABC内接于⊙G,AB是⊙G的直径,AB=2,AC=1,现将制作的几何探究工具放在平面直角坐标系中(如图2),然后点A在x轴上由点O开始向右滑动,点B在y轴上也随之向点O滑动(如图3),并且保持点O在⊙G上,当点B滑动至与点O重合时运动结束.在整个运动过程中,点C运动的路程是3-$\sqrt{3}$.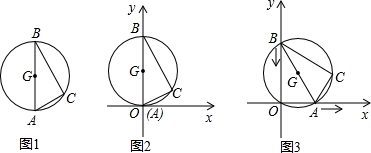
分析 由于在运动过程中,原点O始终在⊙G上,则弧AC的长保持不变,弧AC所对应的圆周角∠AOC保持不变,等于∠XOC,故点C在与x轴夹角为∠ABC的射线上运动.顶点C的运动轨迹应是一条线段,且点C移动到图中C2位置最远,然后又慢慢移动到C3结束,点C经过的路程应是线段C1C2+C2C3.
解答 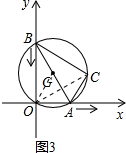 解:如图3,连接OG.
解:如图3,连接OG.
∵∠AOB是直角,G为AB中点,
∴GO=$\frac{1}{2}$AB=半径,
∴原点O始终在⊙G上.
∵∠ACB=90°,AB=2,AC=1,
∴BC=$\sqrt{3}$.
连接OC.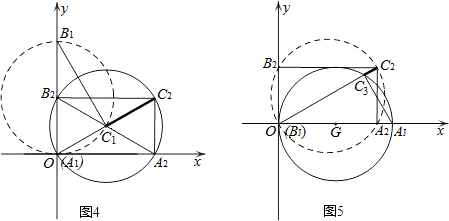 则∠AOC=∠ABC,
则∠AOC=∠ABC,
∴tan∠AOC=$\frac{AC}{BC}$=$\frac{\sqrt{3}}{3}$,
∴点C在与x轴夹角为∠AOC的射线上运动.
如图4,C1C2=OC2-OC1=2-1=1;
如图5,C2C3=OC2-OC3=2-$\sqrt{3}$;
∴总路径为:C1C2+C2C3=1+2-$\sqrt{3}$=3-$\sqrt{3}$.
故答案为:3-$\sqrt{3}$.
点评 此题主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数图象的性质和交点的意义求出相应的线段的长度或表示线段的长度,再结合具体图形的性质求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.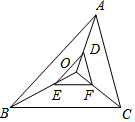 如图,在O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且$\frac{OD}{AD}$=$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,则$\frac{EF}{BC}$=( )
如图,在O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且$\frac{OD}{AD}$=$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,则$\frac{EF}{BC}$=( )
 如图,在O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且$\frac{OD}{AD}$=$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,则$\frac{EF}{BC}$=( )
如图,在O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且$\frac{OD}{AD}$=$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,则$\frac{EF}{BC}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
9.一个三角形三个内角的度数之比为3:4:5,这个三角形一定是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰三角形 |
13.已知点P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2009的值为( )
| A. | (-3)2009 | B. | -1 | C. | 0 | D. | 1 |
11.做一个三角形的木架,以下四组木棒中,符合条件的是( )
| A. | 1cm,2cm,3.5cm | B. | 3cm,4cm,6cm | C. | 4cm,5cm,9cm | D. | 3cm,3cm,6cm |
 如图,某数学兴趣小组将一段长为4的铁丝,围成以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形的最大面积为1.
如图,某数学兴趣小组将一段长为4的铁丝,围成以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形的最大面积为1.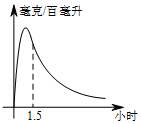 实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示,1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示)
实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示,1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示)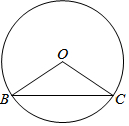 在⊙O中,己知弦BC所对的圆周角∠BAC与圆心角∠BOC互补.
在⊙O中,己知弦BC所对的圆周角∠BAC与圆心角∠BOC互补.