题目内容
4.解下列一元一次不等式(组):(1)4x+1≤8-3x,并把解在数轴上表示出来.
(2)$\left\{\begin{array}{l}3-5x<x-2({2x-1})\\ \frac{3x-2}{4}≤2.5-\frac{x}{2}\end{array}\right.$.
分析 (1)利用移项、合并解一元一次不等式,然后用数轴表示解集;
(2)分别解两个不等式得到x>$\frac{1}{2}$和x≤$\frac{12}{5}$,然后根据大小小大中间找确定不等式组的解集.
解答 解:(1)7x≤8,
x≤1,
用数轴表示为: ;
;
(2)$\left\{\begin{array}{l}{3-5x<x-2(2x-1)①}\\{\frac{3x-2}{4}≤2.5-\frac{x}{2}②}\end{array}\right.$,
解①得x>$\frac{1}{2}$,
解②得x≤$\frac{12}{5}$,
所以不等式组的解集为$\frac{1}{2}$<x≤$\frac{12}{5}$.
点评 本题考查了解一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
15.若a<b,则下列不等式成立的是( )
| A. | ma<mb | B. | 2a>2b | C. | -2a>-2b | D. | $\frac{a}{2}$>$\frac{b}{2}$ |
12.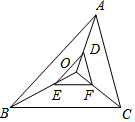 如图,在O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且$\frac{OD}{AD}$=$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,则$\frac{EF}{BC}$=( )
如图,在O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且$\frac{OD}{AD}$=$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,则$\frac{EF}{BC}$=( )
 如图,在O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且$\frac{OD}{AD}$=$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,则$\frac{EF}{BC}$=( )
如图,在O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且$\frac{OD}{AD}$=$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,则$\frac{EF}{BC}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
19.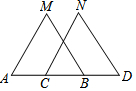 如图,在△ABM和△CDN中,A,C,B,D在同一条直线上,MB=ND,MA=NC,则下列条件中能判定△ABM≌△CDN的是( )
如图,在△ABM和△CDN中,A,C,B,D在同一条直线上,MB=ND,MA=NC,则下列条件中能判定△ABM≌△CDN的是( )
 如图,在△ABM和△CDN中,A,C,B,D在同一条直线上,MB=ND,MA=NC,则下列条件中能判定△ABM≌△CDN的是( )
如图,在△ABM和△CDN中,A,C,B,D在同一条直线上,MB=ND,MA=NC,则下列条件中能判定△ABM≌△CDN的是( )| A. | ∠MAB=∠NCD | B. | ∠MBA=∠NDC | C. | AC=BD | D. | AM∥CN |
9.一个三角形三个内角的度数之比为3:4:5,这个三角形一定是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰三角形 |
13.已知点P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2009的值为( )
| A. | (-3)2009 | B. | -1 | C. | 0 | D. | 1 |
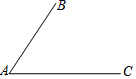 如图,已知线段AB,AC
如图,已知线段AB,AC