题目内容
5.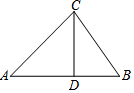 如图,在△ABC中,CD⊥AB于点D,己知AC=a,∠A=α,∠B=β,则BD的长是( )
如图,在△ABC中,CD⊥AB于点D,己知AC=a,∠A=α,∠B=β,则BD的长是( )| A. | $\frac{a•sinα}{tanβ}$ | B. | $\frac{a•cosα}{tanβ}$ | C. | a•sinα•tanβ | D. | a•cosα•tanβ |
分析 在直角△ACD中首先利用正弦定义求得CD的长,然后在直角△BCD中利用正切函数定义求得BD的长.
解答 解:∵在直角△ACD中,sinA=$\frac{CD}{AC}$,即sinα=$\frac{CD}{a}$,
∴CD=asinα.
∵直角△BCD中,tanB=$\frac{CD}{BD}$,即$\frac{CD}{BD}=tanβ$,
∴BD=$\frac{CD}{tanβ}$=$\frac{asinα}{tanβ}$.
故选A.
点评 本题考查了锐角三角函数,正确理解三角函数的定义是关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
15.若a<b,则下列不等式成立的是( )
| A. | ma<mb | B. | 2a>2b | C. | -2a>-2b | D. | $\frac{a}{2}$>$\frac{b}{2}$ |
13.已知点P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2009的值为( )
| A. | (-3)2009 | B. | -1 | C. | 0 | D. | 1 |
17.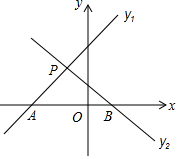 如图,已知直线y1=k1x+m和直线y2=k2x+n交于点P(-1,2),则关于x的不等式(k1-k2)x>-m+n的解是( )
如图,已知直线y1=k1x+m和直线y2=k2x+n交于点P(-1,2),则关于x的不等式(k1-k2)x>-m+n的解是( )
 如图,已知直线y1=k1x+m和直线y2=k2x+n交于点P(-1,2),则关于x的不等式(k1-k2)x>-m+n的解是( )
如图,已知直线y1=k1x+m和直线y2=k2x+n交于点P(-1,2),则关于x的不等式(k1-k2)x>-m+n的解是( )| A. | x>2 | B. | x>-1 | C. | -1<x<2 | D. | x<-1 |
 如图,在?ABCD中,P,Q分别是AD,BC的中点,求证:AC与PQ互相平分.
如图,在?ABCD中,P,Q分别是AD,BC的中点,求证:AC与PQ互相平分.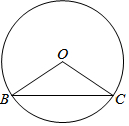 在⊙O中,己知弦BC所对的圆周角∠BAC与圆心角∠BOC互补.
在⊙O中,己知弦BC所对的圆周角∠BAC与圆心角∠BOC互补.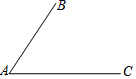 如图,已知线段AB,AC
如图,已知线段AB,AC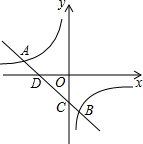 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-3,1),B(2,n)两点,直线AB分别交x轴、y轴于D,C两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-3,1),B(2,n)两点,直线AB分别交x轴、y轴于D,C两点.