题目内容
14．在Rt△ABC中，∠C=90°，AB=6，cosB=$\frac{2}{3}$，则BC的长为（ ）| A． | 4 | B． | $2\sqrt{5}$ | C． | $\frac{{18\sqrt{3}}}{13}$ | D． | $\frac{{12\sqrt{3}}}{13}$ |
分析 根据cosB=$\frac{BC}{AB}$知BC=ABcosB，即可得解．
解答 解：如图，
∵∠C=90°，
∴cosB=$\frac{BC}{AB}$，
∴BC=ABcosB=6×$\frac{2}{3}$=4，
故选：A．
点评 本题主要考查解直角三角形，熟练掌握三角函数的定义是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
4．若抛物线y=x2-2x+m与x轴有交点，则m的取值范围是（ ）
| A． | m＞1 | B． | m≥1 | C． | m＜1 | D． | m≤1 |
5．已知2m=a，2n=b，则23m-n=（ ）
| A． | a3-b | B． | $\frac{{a}^{3}}{b}$ | C． | 3a-b | D． | $\frac{3a}{b}$ |
2．关于直线l：y=kx+k（k≠0），下列说法正确的是（ ）
| A． | l经过定点（1，0） | B． | l经过定点（-1，0） | ||
| C． | l经过第二、三、四象限 | D． | l经过第一、二、三象限 |
9．为了响应我市的“绿色家园”行动，某村计划在荒山上种植1200棵树，原计划每天种x棵，由于邻村的支援，每天比原计划多种了40棵，结果提前了5天完成了任务，则可以列出方程为（ ）
| A． | $\frac{1200}{x}$-$\frac{1200}{x-40}$=5 | B． | $\frac{1200}{x-40}$-$\frac{1200}{x}$=5 | ||
| C． | $\frac{1200}{x+40}$-$\frac{1200}{x}$=5 | D． | $\frac{1200}{x}$-$\frac{1200}{x+40}$=5 |
19．在平面直角坐标系中，抛物线y=-（x-1）2+2的顶点坐标是（ ）
| A． | （-1，2） | B． | （1，2） | C． | （2，-1） | D． | （2，1） |
6．
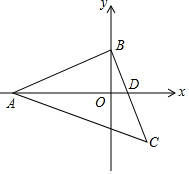如图，在等腰Rt△ABC中，∠ABC=90°，A（p，0），B（0，r），点C在第四象限，BC与x轴交于点D（q，0），x轴恰好平分∠BAC，则点C的坐标为（ ）
如图，在等腰Rt△ABC中，∠ABC=90°，A（p，0），B（0，r），点C在第四象限，BC与x轴交于点D（q，0），x轴恰好平分∠BAC，则点C的坐标为（ ）| A． | （r，$\frac{p-q}{2}$） | B． | （-$\frac{p}{2}$，$\frac{p-q}{2}$） | C． | （r，p+q） | D． | （2q，$\frac{p-r}{2}$） |
如图，大正方形的边长为a，小正方形的边长为b．
如图，半径为5的⊙O中，弦AB，CD所对的圆心角分别是∠AOB，∠COD．已知CD=6，∠AOB+∠COD=180°，则弦AB的弦心距等于3．