题目内容
13．
如图，半径为5的⊙O中，弦AB，CD所对的圆心角分别是∠AOB，∠COD．已知CD=6，∠AOB+∠COD=180°，则弦AB的弦心距等于3．
分析 首先作OF⊥AB于F，作直径BE，连接AE，进而得出AE=DC，再利用三角形中位线的性质得出答案．
解答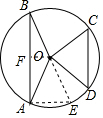 
解：作OF⊥AB于F，作直径BE，连接AE，如图，
∵∠AOB+∠COD=180°，
而∠AOE+∠AOB=180°，
∴∠AOE=∠COD，
∴$\widehat{AE}$=$\widehat{DC}$，
∴AE=DC=6，
∵OF⊥AB，
∴BF=AF，
而OB=OE，
∴OF为△ABE的中位线，
∴OF=$\frac{1}{2}$AE=3．
故答案为：3．
点评 本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了垂径定理和三角形中位线性质．
练习册系列答案
相关题目
14．在Rt△ABC中，∠C=90°，AB=6，cosB=$\frac{2}{3}$，则BC的长为（ ）
| A． | 4 | B． | $2\sqrt{5}$ | C． | $\frac{{18\sqrt{3}}}{13}$ | D． | $\frac{{12\sqrt{3}}}{13}$ |
在平面直角坐标系中，过格点A、B、C作一圆弧．
5．某水果店用1000元购进甲、乙两种新出产的水果共140kg，这两种水果的进价、售价如表所示：
（1）这两种水果各购进多少千克？
（2）若该水果店按售价售完这批水果，获得的利润是多少元？
（3）如果这批水果是在一天之内按照售价销售完成的，除了进货成本，水果店每天的其它销售费用是0.1元/kg，那么水果店销售这批水果获得的利润是多少？
| 进价（元/kg） | 售价（元/kg） | |
| 甲种 | 5 | 8 |
| 乙种 | 9 | 13 |
（2）若该水果店按售价售完这批水果，获得的利润是多少元？
（3）如果这批水果是在一天之内按照售价销售完成的，除了进货成本，水果店每天的其它销售费用是0.1元/kg，那么水果店销售这批水果获得的利润是多少？
如图，C为射线AB上一点，AB=30，AC比BC的$\frac{1}{4}$多5，P，Q两点分别从A，B两点同时出发．分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动，运动时间为t秒，M为BP的中点，N为QM的中点，以下结论：