题目内容
4.若抛物线y=x2-2x+m与x轴有交点,则m的取值范围是( )| A. | m>1 | B. | m≥1 | C. | m<1 | D. | m≤1 |
分析 根据判别式的意义得到△=(-2)2-4m≥0,然后解不等式即可.
解答 解:根据题意得△=(-2)2-4m≥0,
解得m≤1.
故选D.
点评 本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
14.下列计算正确的是( )
| A. | a2+a2=a4 | B. | a8÷a2=a4 | C. | (-a)2-a2=0 | D. | a2•a3=a6 |
15.下列等式从左到右的变形,属于因式分解的是( )
| A. | a(x-y)=ax-ay | B. | x3-x=x(x+1)(x-1) | C. | (x+1)(x+3)=x2+4x+3 | D. | x2+2x+1=x(x+2)+1 |
12.2016年6月13日,保定市首届中学生校园足球比赛在保定一中开幕,参加比赛的共有23支代表队,其中初中男生队有8(A-H)支代表队,若从这8支代表队中随机抽取两支进行一场比赛,则恰好抽到A代表队和C代表队的概率是( )
| A. | $\frac{1}{28}$ | B. | $\frac{1}{32}$ | C. | $\frac{1}{56}$ | D. | $\frac{1}{64}$ |
19.以下选项是二次函数f(x)=x2+(m-3)x+1的图象与x轴的交点(x1,0)(x2,0)均在A(1,0)右侧的充要条件的是( )
| A. | $\left\{\begin{array}{l}f(1)>0\\ \frac{3-m}{2}>1\\△≥0\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x_1}+{x_2}>2\\{x_1}{x_2}>1\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}f(1)>0\\ \frac{3-m}{2}>2\\△>0\end{array}\right.$ | D. | $\left\{\begin{array}{l}f(1)<0\\△>0\end{array}\right.$ |
9.下面四个图形中,既是轴对称又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16.下列各式成立的是( )
| A. | $\sqrt{9}=±3$ | B. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | C. | $\sqrt{{{(-3)}^2}}=-3$ | D. | ${(-\sqrt{3})^2}=3$ |
14.在Rt△ABC中,∠C=90°,AB=6,cosB=$\frac{2}{3}$,则BC的长为( )
| A. | 4 | B. | $2\sqrt{5}$ | C. | $\frac{{18\sqrt{3}}}{13}$ | D. | $\frac{{12\sqrt{3}}}{13}$ |
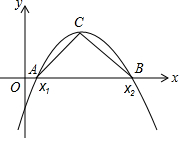 如图,抛物线y=(1-m)x2+4x-3的开口向下,与x轴交于A(x1,0),B(x2,0)两点,其中x1≤x2
如图,抛物线y=(1-m)x2+4x-3的开口向下,与x轴交于A(x1,0),B(x2,0)两点,其中x1≤x2