题目内容
2.关于直线l:y=kx+k(k≠0),下列说法正确的是( )| A. | l经过定点(1,0) | B. | l经过定点(-1,0) | ||
| C. | l经过第二、三、四象限 | D. | l经过第一、二、三象限 |
分析 将点的坐标代入直线的解析式可判断A、B;根据一次函数图象与系数的关系可判断C、D.
解答 解:第一种方法:A、∵x=1时,y=k+k=2k≠0,∴l不经过点(1,0),故本选项错误;
B、∵x=-1时,y=-k+k=0,∴l经过点(-1,0),故本选项正确;
C、当k<0时,直线y=kx+k经过第二、三、四象限,故本选项错误;
D、当k>0时,直线y=kx+k经过第一、二、三象限,故本选项错误;
第二种方法:y=kx+k=k(x+1),令x+1=0,得出y=0,x=-1,则l经过定点(-1,0).
故选B.
点评 本题主要考查了一次函数图象在坐标平面内的位置与k、b的关系.解答本题注意理解:直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限.k<0时,直线必经过二、四象限.b>0时,直线与y轴正半轴相交.b=0时,直线过原点;b<0时,直线与y轴负半轴相交.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
12.2016年6月13日,保定市首届中学生校园足球比赛在保定一中开幕,参加比赛的共有23支代表队,其中初中男生队有8(A-H)支代表队,若从这8支代表队中随机抽取两支进行一场比赛,则恰好抽到A代表队和C代表队的概率是( )
| A. | $\frac{1}{28}$ | B. | $\frac{1}{32}$ | C. | $\frac{1}{56}$ | D. | $\frac{1}{64}$ |
10.某时装标价为650元,某女士在”双十一“中以标价5折少30元的价钱购得,此时店主仍净赚50元,此时装进价为( )
| A. | 275元 | B. | 295元 | C. | 245元 | D. | 325元 |
17.观察表1,寻找规律,表2是从表1中截取的一部分,其中a,b,c的值分别为( )
表1:
表2:
表1:
| 1 | 2 | 3 | 4 | … |
| 2 | 4 | 6 | 8 | … |
| 3 | 6 | 9 | 12 | … |
| 4 | 8 | 12 | 16 | … |
| … | … | … | … | … |
| 20 | a |
| 24 | b |
| c | 35 |
| A. | 15,18,28 | B. | 22,27,25 | C. | 24,30,28 | D. | 25,30,28 |
7.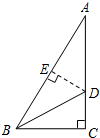 如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若CD=3cm,则点D到AB的距离DE是( )
如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若CD=3cm,则点D到AB的距离DE是( )
 如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若CD=3cm,则点D到AB的距离DE是( )
如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若CD=3cm,则点D到AB的距离DE是( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
14.在Rt△ABC中,∠C=90°,AB=6,cosB=$\frac{2}{3}$,则BC的长为( )
| A. | 4 | B. | $2\sqrt{5}$ | C. | $\frac{{18\sqrt{3}}}{13}$ | D. | $\frac{{12\sqrt{3}}}{13}$ |
11.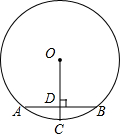 如图,AB为⊙O的弦,AB=6cm,OC⊥AB于D,交⊙O于点C,且CD=1cm,则⊙O的半径为( )
如图,AB为⊙O的弦,AB=6cm,OC⊥AB于D,交⊙O于点C,且CD=1cm,则⊙O的半径为( )
 如图,AB为⊙O的弦,AB=6cm,OC⊥AB于D,交⊙O于点C,且CD=1cm,则⊙O的半径为( )
如图,AB为⊙O的弦,AB=6cm,OC⊥AB于D,交⊙O于点C,且CD=1cm,则⊙O的半径为( )| A. | 5cm | B. | 6cm | C. | 8cm | D. | 10cm |
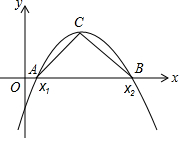 如图,抛物线y=(1-m)x2+4x-3的开口向下,与x轴交于A(x1,0),B(x2,0)两点,其中x1≤x2
如图,抛物线y=(1-m)x2+4x-3的开口向下,与x轴交于A(x1,0),B(x2,0)两点,其中x1≤x2