题目内容
12. 如图,大正方形的边长为a,小正方形的边长为b.
如图,大正方形的边长为a,小正方形的边长为b.(1)求阴影部分的面积S.
(2)如果a+b=4,ab=2,求S的值.
分析 (1)根据题意和图形可知阴影部分的面积是大正方形的面积加上小正方形的面积再减去△AGF和△ACD的面积,然后用相应的代数式表示出来即可解答本题;
(2)将(1)中S的代数式变形,然后将a+b=4,ab=2,代入即可解答本题.
解答 解:(1)由图可得,
阴影部分的面积S是:${a}^{2}+{b}^{2}-\frac{{a}^{2}}{2}-\frac{(a+b)b}{2}$=$\frac{{a}^{2}}{2}+\frac{{b}^{2}}{2}-\frac{ab}{2}$,
即阴影部分的面积S是$\frac{{a}^{2}}{2}+\frac{{b}^{2}}{2}-\frac{ab}{2}$;
(2)∵a+b=4,ab=2,
∴S=$\frac{{a}^{2}}{2}+\frac{{b}^{2}}{2}-\frac{ab}{2}$=$\frac{{a}^{2}+{b}^{2}}{2}-\frac{ab}{2}$=$\frac{(a+b)^{2}-2ab}{2}-\frac{ab}{2}$=$\frac{{4}^{2}-2×2}{2}-\frac{2}{2}$=5,
即如果a+b=4,ab=2,S的值是5.
点评 本题考查整式的混合运算、代数式求值,解题的关键是明确题意,用相应的代数式表示出阴影部分的面积,会求代数式的值.

练习册系列答案
相关题目
14.在Rt△ABC中,∠C=90°,AB=6,cosB=$\frac{2}{3}$,则BC的长为( )
| A. | 4 | B. | $2\sqrt{5}$ | C. | $\frac{{18\sqrt{3}}}{13}$ | D. | $\frac{{12\sqrt{3}}}{13}$ |
11.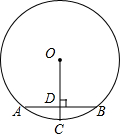 如图,AB为⊙O的弦,AB=6cm,OC⊥AB于D,交⊙O于点C,且CD=1cm,则⊙O的半径为( )
如图,AB为⊙O的弦,AB=6cm,OC⊥AB于D,交⊙O于点C,且CD=1cm,则⊙O的半径为( )
 如图,AB为⊙O的弦,AB=6cm,OC⊥AB于D,交⊙O于点C,且CD=1cm,则⊙O的半径为( )
如图,AB为⊙O的弦,AB=6cm,OC⊥AB于D,交⊙O于点C,且CD=1cm,则⊙O的半径为( )| A. | 5cm | B. | 6cm | C. | 8cm | D. | 10cm |
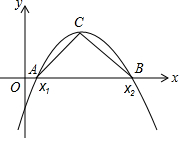 如图,抛物线y=(1-m)x2+4x-3的开口向下,与x轴交于A(x1,0),B(x2,0)两点,其中x1≤x2
如图,抛物线y=(1-m)x2+4x-3的开口向下,与x轴交于A(x1,0),B(x2,0)两点,其中x1≤x2 如图,C为射线AB上一点,AB=30,AC比BC的$\frac{1}{4}$多5,P,Q两点分别从A,B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论:
如图,C为射线AB上一点,AB=30,AC比BC的$\frac{1}{4}$多5,P,Q两点分别从A,B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论: