题目内容
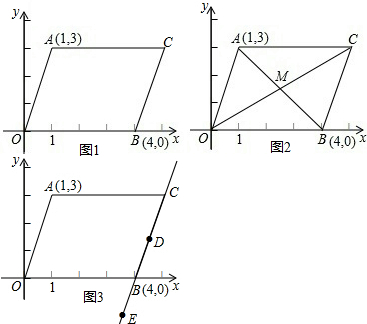
平行四边形AOBC在平面直角坐标系中的位置如图(1).
(1)写出点C的坐标;
(2)在图(1)中,连接AB,OC得到图(2),求AB与OC的交点M点的坐标;
(3)将图(2)中的线段BC向两方延长得到图(3),若点D,E为直线BC上不与B,C重合的动点,是否存在这样的D,E点,使得四边形OADE为矩形?若存在,请在图中画出矩形,并求出矩形OADE的面积和点D,E的坐标,若不存在,请说明理由.
(1)写出点C的坐标;
(2)在图(1)中,连接AB,OC得到图(2),求AB与OC的交点M点的坐标;
(3)将图(2)中的线段BC向两方延长得到图(3),若点D,E为直线BC上不与B,C重合的动点,是否存在这样的D,E点,使得四边形OADE为矩形?若存在,请在图中画出矩形,并求出矩形OADE的面积和点D,E的坐标,若不存在,请说明理由.

考点:四边形综合题
专题:
分析:(1)根据平行四边形的对边相等和已知点的坐标求得点C的坐标即可;
(2)首先求得直线AB的解析式,然后得到直线OC的解析式,联立后即可求得交点M的坐标;
(3)分别过点A、O作AD⊥BC于点D,OE⊥BC于点E,过E、D分别作x轴的垂线,垂足分别为F、G,利用四边形AOBC是平行四边形,得到AO∥BC,从而得到四边形AOED是矩形,且与平行四边形AOBC面积相等,从而求得矩形AOED的面积为12,求得线段EF和线段OF后即可求得点E的坐标,从而求得点D的坐标.
(2)首先求得直线AB的解析式,然后得到直线OC的解析式,联立后即可求得交点M的坐标;
(3)分别过点A、O作AD⊥BC于点D,OE⊥BC于点E,过E、D分别作x轴的垂线,垂足分别为F、G,利用四边形AOBC是平行四边形,得到AO∥BC,从而得到四边形AOED是矩形,且与平行四边形AOBC面积相等,从而求得矩形AOED的面积为12,求得线段EF和线段OF后即可求得点E的坐标,从而求得点D的坐标.
解答:解:(1)∵四边形OACB是平行四边形,
∴AC=OB,
∵A(1,3)、B(4,0),
∴C(5,3);
(2)如图(2),设AB所在的直线的解析式为y=kx+b,
∵直线AB经过点A(1,3)、B(4,0),
∴
,
∴AB所在直线的解析式为y=-4x+4,
由于OC所在直线的表达式为y=
x,
联立方程
解得:
即M的坐标是(2.5,1.5);
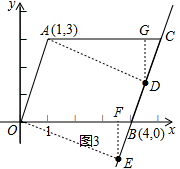
(3)存在这样的D、E,使得四边形AOED是矩形.
分别过点A、O作AD⊥BC于点D,OE⊥BC于点E,过E、D分别作x轴的垂线,垂足分别为F、G,
∵四边形AOBC是平行四边形,
∴AO∥BC,
∴AD⊥AO,
∴四边形AOED是矩形,且与平行四边形AOBC面积相等,
∵平行四边形AOBC的面积为12,
∴矩形AOED的面积为12,
由勾股定理知AO=
,
∴OE=
,EB=
,
∴EF=
=
=1.2,
OF=
=
=3.6,
∴点E的坐标为(3.6,-1.2),
∴点D的坐标为(4.6,1.8).
∴AC=OB,
∵A(1,3)、B(4,0),
∴C(5,3);
(2)如图(2),设AB所在的直线的解析式为y=kx+b,
∵直线AB经过点A(1,3)、B(4,0),
∴
|
∴AB所在直线的解析式为y=-4x+4,
由于OC所在直线的表达式为y=
| 3 |
| 5 |
联立方程
|
解得:
|
即M的坐标是(2.5,1.5);
(3)存在这样的D、E,使得四边形AOED是矩形.
分别过点A、O作AD⊥BC于点D,OE⊥BC于点E,过E、D分别作x轴的垂线,垂足分别为F、G,
∵四边形AOBC是平行四边形,
∴AO∥BC,
∴AD⊥AO,
∴四边形AOED是矩形,且与平行四边形AOBC面积相等,
∵平行四边形AOBC的面积为12,
∴矩形AOED的面积为12,
由勾股定理知AO=
| 10 |
∴OE=
| 12 | ||
|
| 4 | ||
|
∴EF=
| EB•OE |
| OB |
| ||||||||
| 4 |
OF=
| OE2-EF2 |
|
∴点E的坐标为(3.6,-1.2),
∴点D的坐标为(4.6,1.8).

点评:此题主要考查四边形的综合知识、勾股定理等知识,综合性较强,而且有一定的拔高难度,属于难题,要求学生做题时一定要仔细,认真.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
已知⊙O与直线AB相交,且圆心O到直线AB的距离是方程2x-1=4的根,则⊙O的半径可为( )
| A、1 | B、2 | C、2.5 | D、3 |
 如图,AB∥CD,且∠D=70°,CD=BC,则∠ABC的度数为
如图,AB∥CD,且∠D=70°,CD=BC,则∠ABC的度数为
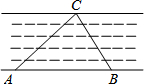 如图,为了测量不能到达对岸的河宽,在河的岸边选两点A、B,测得AB=100米,分别在A点和B点看对岸一点C,测得∠A=43°,∠B=65°,求河宽(河宽可看成是点C到直线AB的距离).
如图,为了测量不能到达对岸的河宽,在河的岸边选两点A、B,测得AB=100米,分别在A点和B点看对岸一点C,测得∠A=43°,∠B=65°,求河宽(河宽可看成是点C到直线AB的距离). 定义:如果一个的函数图象经过平移后能与反比例函数y=
定义:如果一个的函数图象经过平移后能与反比例函数y=