题目内容

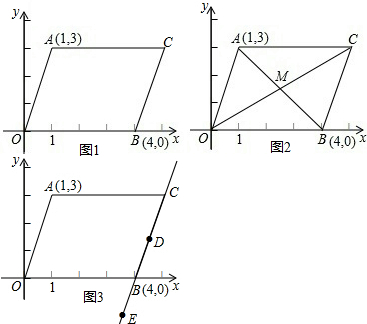
如图，AB∥CD，且∠D=70°，CD=BC，则∠ABC的度数为
 
．
考点：平行线的性质
专题：
分析：先由等边对等角得到∠D=∠CBD=70°，再根据三角形内角和定理求出∠C=40°，根据两直线平行，内错角相等得出∠ABC=∠C=40°．
解答：解：∵CD=BC，
∴∠D=∠CBD=70°，
∵∠CBD+∠C+∠D=180°，
∴∠C=180°-70°×2=40°．
∵AB∥CD，
∴∠ABC=∠C=40°．
故答案为：40°．
点评：本题考查了三角形内角和定理及平行线的性质，是基础题，比较简单．
练习册系列答案
相关题目
阅读材料：
小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如3+2
2
=（1+
2
）2．善于思考的小明进行了以下探索：
设a+b
2
=（m+n
2
）2（其中a、b、m、n均为整数），则有a+b
2
=m2+2n2+2mn
2
．
∴a=m2+2n2，b=2mn．这样小明就找到了一种把类似a+b
2
的式子化为平方式的方法．
请你仿照小明的方法探索并解决下列问题：
（1）当a、b、m、n均为正整数时，若a+b
3
=（m+n
3
）2，用含m、n的式子分别表示a、b，得：a=
 
，b=
 
；
（2）利用所探索的结论，请找一组正整数a、b、m、n填空：
 
+
 
3
=（
 
+
 
3
）2；
（3）若a-6
5
=（m-n
5
）2且a、m、n均为正整数，求a的值．
已知关于x的方程3x+2a-3=0的解是x=3，则a的值为
 
．
有五张下面分别标有数字-2，0，
1
2
，1，3的不透明卡片，它们除数字不同外其余全部相同．现将它们背面朝上，洗匀后从中任取一张，将该卡片上的数字记为a，则使关于x的分工方程
1-ax
x-2
+2=
1
2-x
有整数解的概率是
 
．
已知最简二次根式
2a-4
与
2
是同类二次根式，则a的值为
 
．
已知不等式x≤a的解集中有4个非负整数，则a的取值范围为：
 
．
不等式2（x-3）≤2a+1的自然数解只有0、1、2三个，则a的取值范围是
 
．
若不等式组
x＞a
9-5x
4
＞1
无解，则a的取值范围是（　　）
A、a＜1B、a=1
C、a＞1D、a≥1
平行四边形AOBC在平面直角坐标系中的位置如图（1）．
（1）写出点C的坐标；
（2）在图（1）中，连接AB，OC得到图（2），求AB与OC的交点M点的坐标；
（3）将图（2）中的线段BC向两方延长得到图（3），若点D，E为直线BC上不与B，C重合的动点，是否存在这样的D，E点，使得四边形OADE为矩形？若存在，请在图中画出矩形，并求出矩形OADE的面积和点D，E的坐标，若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网