题目内容
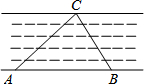如图，为了测量不能到达对岸的河宽，在河的岸边选两点A、B，测得AB=100米，分别在A点和B点看对岸一点C，测得∠A=43°，∠B=65°，求河宽（河宽可看成是点C到直线AB的距离）．考点：解直角三角形的应用
专题：
分析：通过解Rt△ACD和Rt△BCD求得AD、BD的长度，然后由AB=100米列出关于CD的方程，通过解方程可以求得CD的长度．
解答：
解：作CD⊥AB于D．
∵tanA=
，tanB=
，
∴AD=
=
，BD=
=
．
又∵AD+DB=AB，AB=100
∴
+
=100．
∴CD=
≈64.99（或65.0）
答：河的宽度约是65.0米．
解：作CD⊥AB于D．∵tanA=
| CD |
| AD |
| CD |
| BD |
∴AD=
| CD |
| tanA |
| CD |
| tan43° |
| CD |
| tanB |
| CD |
| tan65° |
又∵AD+DB=AB，AB=100
∴
| CD |
| tan43° |
| CD |
| tan65° |
∴CD=
| 100 | ||||
|
答：河的宽度约是65.0米．
点评：本题考查了解直角三角形的应用．主要是正切概念及运算，关键把实际问题转化为数学问题加以计算．
练习册系列答案
相关题目
如果把分式
中的x，y都扩大为原来的2倍，则分式的值（ ）
| xy |
| y-x |
| A、扩大为原来的2倍 | ||
| B、扩大为原来的4倍 | ||
C、缩小为原来的
| ||
| D、不变 |
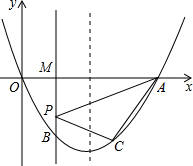如图，抛物线y=x2-2mx（m＞0）与x轴的另一个交点为A，过P（1，-m）作PM⊥x轴于点M，交抛物线于点B．点B关于抛物线对称轴的对称点为C．
如图，已知△ABC中，点D、E、F分别是AB、AC、BC上的点，DE∥BC，EF∥AB．