题目内容
6．不等式组$\left\{\begin{array}{l}{-3x+2＜x-6}\\{x＞m}\end{array}\right.$的解集是x＞2，那么m的取值范围（ ）| A． | m＞2 | B． | m＜2 | C． | m≥2 | D． | m≤2 |
分析 求出第一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了结合不等式组的解集可得m的范围．
解答 解：解不等式-3x+2＜x-6，得：x＞2，
∵不等式组的解集是x＞2，
∴m≤2，
故选：D．
点评 本题考查的是解一元一次不等式组，正确求出第一个不等式解集是前提，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
17．分式$-\frac{1}{{6{x^2}y}}$和$\frac{1}{2xyz}$最简公分母是（ ）
| A． | -6xyz | B． | 6x2yz | C． | 12xyz | D． | 12x2yz |
14．整式：-0.34x2y，π，$\frac{a+1}{2}$，-52xyz2，$\frac{1}{3}$x2-$\frac{1}{5}$y，-$\frac{1}{3}$xy2-$\frac{1}{2}$中，单项式有（ ）
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
1．
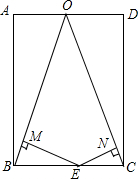如图，在矩形ABCD中，AB=3，BC=2，O是AD的中点，连接OB、OC，点E在线段BC上（点E不与点B、C重合），过点E作EM⊥OB于M，EN⊥OC于N，则EM+EN的值为（ ）
如图，在矩形ABCD中，AB=3，BC=2，O是AD的中点，连接OB、OC，点E在线段BC上（点E不与点B、C重合），过点E作EM⊥OB于M，EN⊥OC于N，则EM+EN的值为（ ）| A． | 6 | B． | 1.5 | C． | $\frac{3}{10}\sqrt{10}$ | D． | $\frac{3}{5}\sqrt{10}$ |
