题目内容
18.(1)探究发现:下面是一道例题及其解答过程,请补充完整:
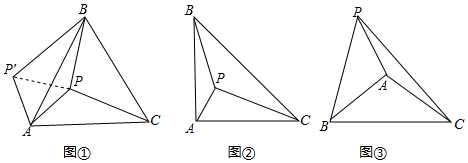
如图①在等边△ABC内部,有一点P,若∠APB=150°.求证:AP2+BP2=CP2
证明:将△APC绕A点逆时针旋转60°,得到△AP′B,连接PP′,则△APP′为等边三角形
∴∠APP′=60° PA=PP′PC=P′B
∵∠APB=150°∴∠BPP′=90°
∴P′P2+BP2=P′B2
即PA2+PB2=PC2
(2)类比延伸:
如图②在等腰三角形ABC中,∠BAC=90°,内部有一点P,若∠APB=135°,试判断线段PA、PB、PC之间的数量关系,并证明.
(3)联想拓展:
如图③在△ABC中,∠BAC=120°,AB=AC,点P在直线AB上方,且∠APB=60°,满足(kPA)2+PB2=PC2,请直接写出k的值.
分析 (1)根据旋转的性质和勾股定理直接写出即可;
(2)将△APC绕A点逆时针旋转90°,得到△AP′B,连接PP′,论证PP′=$\sqrt{2}$PA,再根据勾股定理代换即可;
(3)将△APC 绕A点顺时针旋转120°得到△AP′B,连接PP′,过点A作AH⊥PP′,论证PP′=$\sqrt{3}$PA,再根据勾股定理代换即可.
解答 解:(1)PC=P′B
P′P2+BP2=P′B2.
(2)关系式为:2PA2+PB2=PC2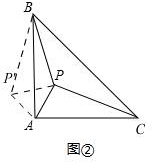
证明如图②:将△APC绕A点逆时针旋转90°,得到△AP′B,连接PP′,
则△APP′为等腰直角三角形
∴∠APP′=45°PP′=$\sqrt{2}$PA,PC=P′B,
∵∠APB=135°
∴∠BPP′=90°
∴P′P2+BP2=P′B2,
∴2PA2+PB2=PC2
(3)k=$\sqrt{3}$.
证明:如图③
将△APC 绕A点顺时针旋转120°得到△AP′B,连接PP′,过点A作AH⊥PP′,
可得∠APP′=30°PP′=$\sqrt{3}$PA,PC=P′B,
∵∠APB=60°,
∴∠BPP′=90°,
∴P′P2+BP2=P′B2,
∴($\sqrt{3}$PA)2+PB2=PC2
∵(kPA)2+PB2=PC2,
∴k=$\sqrt{3}$.
点评 此题主要考查几何变换中的旋转变换,熟悉旋转变换的性质,并通过旋转构造直角三角形运用勾股定理是解题的关键.

练习册系列答案
相关题目
8.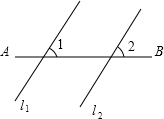 如图,将直线l1沿AB的方向平移得到l2,若∠1=40°,则∠2=( )
如图,将直线l1沿AB的方向平移得到l2,若∠1=40°,则∠2=( )
 如图,将直线l1沿AB的方向平移得到l2,若∠1=40°,则∠2=( )
如图,将直线l1沿AB的方向平移得到l2,若∠1=40°,则∠2=( )| A. | 40° | B. | 50° | C. | 90° | D. | 140° |
6.不等式组$\left\{\begin{array}{l}{-3x+2<x-6}\\{x>m}\end{array}\right.$的解集是x>2,那么m的取值范围( )
| A. | m>2 | B. | m<2 | C. | m≥2 | D. | m≤2 |
7.正比例函数y=2x的图象与反比例函数y=$\frac{3}{x}$的图象的交点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第一、三象限 | D. | 第二、四象限 |
 如图,它是由哪个基本图形经过怎样的变化得到的?
如图,它是由哪个基本图形经过怎样的变化得到的? 如图,在边长为5cm的正方形纸片ABCD中,点F在边BC上,已知FB=2cm.如果将纸折起,使点A落在点F上,则tan∠GEA=$\frac{5}{2}$.
如图,在边长为5cm的正方形纸片ABCD中,点F在边BC上,已知FB=2cm.如果将纸折起,使点A落在点F上,则tan∠GEA=$\frac{5}{2}$. 如图,已知四边形ABCD内接于⊙O,点O在∠D的内部,∠OAD+∠OCD=50°,则∠B=130°.
如图,已知四边形ABCD内接于⊙O,点O在∠D的内部,∠OAD+∠OCD=50°,则∠B=130°.