题目内容
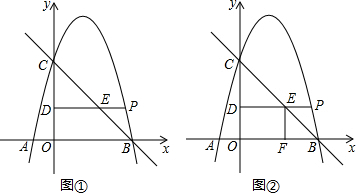
15.如图①,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于点A、B,点A、B的坐标分别是(-1,0)、(4,0),与y轴交于点C,点P在第一、二象限的抛物线上,过点P作x轴的平行线分别交y轴和直线BC于点D、E,设点P的横坐标为m,线段DE的长度为d.(1)求这条抛物线对应的函数表达式;
(2)当点P在第一象限时,求d与m之间的函数关系式;
(3)在(2)的条件下,当PE=2DE时,求m的值;
(4)如图②,过点E作EF∥y轴交x轴于点F,直接写出四边形ODEF的周长不变时m的取值范围.
分析 (1)根据待定系数法,可得函数解析式;
(2)根据自变量与函数值的对应关系,可得C点坐标,根据待定系数法,可得BC的解析式,根据E点的纵坐标,可得E点的横坐标,根据两点间的距离,可得答案;
(3)根据PE与DE的关系,可得关于m的方程,根据解方程根据解方程,可得答案;
(4)根据周长公式,可得答案.
解答 解:(1)由题意,得$\left\{\begin{array}{l}{-(-1)^{2}-b+c=0}\\{-{4}^{2}+4b+c=0}\end{array}\right.$
解得$\left\{\begin{array}{l}{b=3}\\{c=4}\end{array}\right.$
∴这条抛物线对应的函数表达式是y=-x2+3x+4;
(2)当x=0时,y=4.
∴点C的坐标是(0,4).
设直线BC的函数关系式为y=kx+b.
由题意,得$\left\{\begin{array}{l}{b=4}\\{4k+b=0}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=-1}\\{b=4}\end{array}\right.$
∴直线BC的函数关系式为y=-x+4,
∵PD∥x轴,
∴yP=yE=-m2+3m+4..
∴xE=-m2+3m.
图①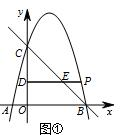 ,
,
当0<m<3时,如图①,d=-m2+3m.
当3<m<4时,如图②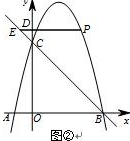 ,d=m2-3m.
,d=m2-3m.
(3)当0<m<3时,DE=-m2+3m,PE=-m2+4m.
∵PE=2DE,
∴-m2+4m=2(-m2+3m).
解得m1=0(不合题意,舍去),m2=2.
当3<m<4时,DE=m2-3m,PE=-m2+4m.
∵PE=2DE,
∴-m2+4m=2(m2-3m).
解得m1=0(不合题意,舍去),m2=$\frac{10}{3}$.
当PE=2DE时,m=2或m=$\frac{10}{3}$.
(4)-1<m<0或3<m<4.
解答如下:当0<m<3时,如图③,DE=-m2+3m,EF=-m2+3m+4.
∴C=2(-m2+3m+4-m2+3m)=-4m2+12m+8.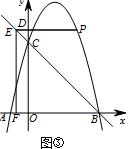
当-1<m<0或3<m<4时,如图④、⑤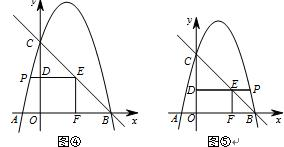 ,
,
DE=m2-3m,EF=-m2+3m+4.
∴C=2(-m2+3m+4+m2-3m)=8.
综上所述:四边形ODEF的周长不变时m的取值范围是-1<m<0或3<m<4.
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式;利用平行于x轴直线上点的纵坐标相等得出E点的纵坐标是解题关键;利用PE与DE的关系得出关于m的方程是解题关键;利用矩形的周长公式是解题关键.

 阅读快车系列答案
阅读快车系列答案| A. | m>2 | B. | m<2 | C. | m≥2 | D. | m≤2 |
| A. | 第一象限 | B. | 第二象限 | C. | 第一、三象限 | D. | 第二、四象限 |
 如图,在边长为5cm的正方形纸片ABCD中,点F在边BC上,已知FB=2cm.如果将纸折起,使点A落在点F上,则tan∠GEA=$\frac{5}{2}$.
如图,在边长为5cm的正方形纸片ABCD中,点F在边BC上,已知FB=2cm.如果将纸折起,使点A落在点F上,则tan∠GEA=$\frac{5}{2}$.
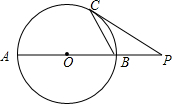 如图,C是⊙O上的一点,过点C的⊙O的切线交直径AB的延长线于点P,若OB=PB=2$\sqrt{3}$,则BC的长为2$\sqrt{3}$.
如图,C是⊙O上的一点,过点C的⊙O的切线交直径AB的延长线于点P,若OB=PB=2$\sqrt{3}$,则BC的长为2$\sqrt{3}$.