题目内容
16.若m、n(m<n)是关于x的方程(x-a)(x-b)+2=0的两根,且a<b,则a,b,m,n的大小关系用“<”连接的结果是a<m<n<b.分析 由于(x-a)(x-b)=-2,于是可m、n看作抛物线y=(x-a)(x-b)与直线y=-2的两交点的横坐标,而抛物线y=(x-a)(x-b)与x轴的两交点坐标为(a,0),(b,0),然后画出函数图象,再利用函数图象即可得到a,b,m,n的大小关系.
解答 解:∵(x-a)(x-b)+2=0,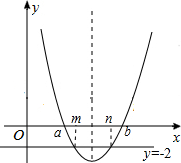
∴(x-a)(x-b)=-2,
∴m、n可看作抛物线y=(x-a)(x-b)与直线y=-2的两交点的横坐标,
∵抛物线y=(x-a)(x-b)与x轴的两交点坐标为(a,0),(b,0),如图,
∴a<m<n<b.
故答案为:a<m<n<b.
点评 本题考查了抛物线与x轴的交点、根与系数的关系;根据题意得出m、n可看作抛物线y=(x-a)(x-b)与直线y=-2的两交点的横坐标是解决问题的关键.

练习册系列答案
相关题目
6.不等式组$\left\{\begin{array}{l}{-3x+2<x-6}\\{x>m}\end{array}\right.$的解集是x>2,那么m的取值范围( )
| A. | m>2 | B. | m<2 | C. | m≥2 | D. | m≤2 |
7.正比例函数y=2x的图象与反比例函数y=$\frac{3}{x}$的图象的交点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第一、三象限 | D. | 第二、四象限 |
11.一个圆锥的侧面展开图是半径为8,圆心角为120°的扇形,则这个圆锥的高为( )
| A. | $\frac{16}{3}\sqrt{2}$cm | B. | $\frac{16}{3}$cm | C. | $\frac{8}{3}\sqrt{2}$cm | D. | $\frac{8}{3}$cm |
1.化简$\frac{{a}^{2}}{a-1}+\frac{1}{1-a}$的结果是( )
| A. | a | B. | a+1 | C. | a-1 | D. | a2-1 |
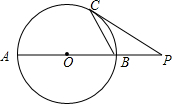 如图,C是⊙O上的一点,过点C的⊙O的切线交直径AB的延长线于点P,若OB=PB=2$\sqrt{3}$,则BC的长为2$\sqrt{3}$.
如图,C是⊙O上的一点,过点C的⊙O的切线交直径AB的延长线于点P,若OB=PB=2$\sqrt{3}$,则BC的长为2$\sqrt{3}$. 如图,已知四边形ABCD内接于⊙O,点O在∠D的内部,∠OAD+∠OCD=50°,则∠B=130°.
如图,已知四边形ABCD内接于⊙O,点O在∠D的内部,∠OAD+∠OCD=50°,则∠B=130°.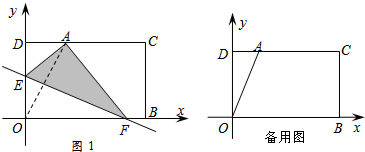
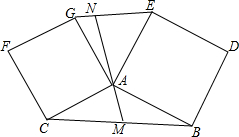 如图,四边形ABDE和ACFG都是正方形,过A作直线l,交BC,GE于M、N.
如图,四边形ABDE和ACFG都是正方形,过A作直线l,交BC,GE于M、N.