题目内容
16.已知:x1、x2是一元二次方程x2-4x+1=0的两个实数根,求:(x12+x22)÷($\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$)的值.分析 根据根与系数的关系得到x1+x2=4,x1x2=1,再利用完全平方公式和通过把原式变形得到[(x1+x2)2-2x1x2]÷$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$,然后利用整体代入的方法计算.
解答 解:根据题意得x1+x2=4,x1x2=1,
所以原式=[(x1+x2)2-2x1x2]÷$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$
=(42-2×1)÷$\frac{4}{1}$
=14÷4
=$\frac{7}{2}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了代数式的变形能力.

练习册系列答案
相关题目
7. 如图所示,已知∠3=∠4,若要使∠1=∠2,则需( )
如图所示,已知∠3=∠4,若要使∠1=∠2,则需( )
 如图所示,已知∠3=∠4,若要使∠1=∠2,则需( )
如图所示,已知∠3=∠4,若要使∠1=∠2,则需( )| A. | ∠1=∠3 | B. | ∠2=∠3 | C. | AB∥CD | D. | ∠1=∠4 |
11.下列各数中,是无理数的是( )
| A. | 0.11 | B. | $\sqrt{12}$ | C. | -$\frac{1}{3}$ | D. | $\root{3}{8}$ |
8.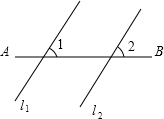 如图,将直线l1沿AB的方向平移得到l2,若∠1=40°,则∠2=( )
如图,将直线l1沿AB的方向平移得到l2,若∠1=40°,则∠2=( )
 如图,将直线l1沿AB的方向平移得到l2,若∠1=40°,则∠2=( )
如图,将直线l1沿AB的方向平移得到l2,若∠1=40°,则∠2=( )| A. | 40° | B. | 50° | C. | 90° | D. | 140° |
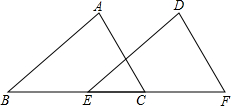 已知,如图,AC=DF,AC∥DF,BE=CF,请写出△ABC≌△DEF的理由.
已知,如图,AC=DF,AC∥DF,BE=CF,请写出△ABC≌△DEF的理由. 如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA向点A运动,当运动到点A时停止,若设点D运动的时间为t秒.点D运动的速度为每秒1个单位长度.
如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA向点A运动,当运动到点A时停止,若设点D运动的时间为t秒.点D运动的速度为每秒1个单位长度.