题目内容
1.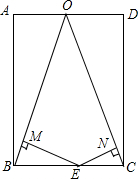 如图,在矩形ABCD中,AB=3,BC=2,O是AD的中点,连接OB、OC,点E在线段BC上(点E不与点B、C重合),过点E作EM⊥OB于M,EN⊥OC于N,则EM+EN的值为( )
如图,在矩形ABCD中,AB=3,BC=2,O是AD的中点,连接OB、OC,点E在线段BC上(点E不与点B、C重合),过点E作EM⊥OB于M,EN⊥OC于N,则EM+EN的值为( )| A. | 6 | B. | 1.5 | C. | $\frac{3}{10}\sqrt{10}$ | D. | $\frac{3}{5}\sqrt{10}$ |
分析 连接OE,由矩形的性质得出CD=AB=3,AD=BC=2,∠A=∠D=90°,由勾股定理得出OB=OC=$\sqrt{10}$,由△OBE的面积+△OCE的面积=△OBC的面积,即可得出结果.
解答 解:连接OE,如图所示: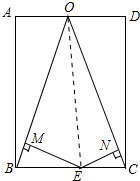
∵四边形ABCD是矩形,
∴CD=AB=3,AD=BC=2,∠A=∠D=90°,
∵O是AD的中点,
∴AO=DO=1,
∴OB=OC=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
∵△OBE的面积+△OCE的面积=△OBC的面积,
∴$\frac{1}{2}$OB•EM+$\frac{1}{2}$OC•EN=$\frac{1}{2}$BC•AB,
∴$\frac{1}{2}$(EM+EN)×$\sqrt{10}$=$\frac{1}{2}$×2×3,
解得:EM+EN=$\frac{3\sqrt{10}}{5}$;
故选:D.
点评 本题考查了矩形的性质、三角形面积的计算;熟记矩形的性质,由三角形的面积关系得出结果是解决问题的关键.

练习册系列答案
相关题目
11.下列各数中,是无理数的是( )
| A. | 0.11 | B. | $\sqrt{12}$ | C. | -$\frac{1}{3}$ | D. | $\root{3}{8}$ |
16.下列计算正确的是( )
| A. | (4x+5y)2=16x2+20xy+25y2 | B. | (-2x3y4z)3=-8x9y12z3 | ||
| C. | (a-b)(a+b)=2a-2b | D. | (-a6)÷(-a)4=a2 |
6.不等式组$\left\{\begin{array}{l}{-3x+2<x-6}\\{x>m}\end{array}\right.$的解集是x>2,那么m的取值范围( )
| A. | m>2 | B. | m<2 | C. | m≥2 | D. | m≤2 |
11.一个圆锥的侧面展开图是半径为8,圆心角为120°的扇形,则这个圆锥的高为( )
| A. | $\frac{16}{3}\sqrt{2}$cm | B. | $\frac{16}{3}$cm | C. | $\frac{8}{3}\sqrt{2}$cm | D. | $\frac{8}{3}$cm |
 如图,菱形ABCD的对角线AC,BD相交于点O,AC=16cm,BD=12cm,则菱形边AB上的高DH的长是9.6cm.
如图,菱形ABCD的对角线AC,BD相交于点O,AC=16cm,BD=12cm,则菱形边AB上的高DH的长是9.6cm. 如图,它是由哪个基本图形经过怎样的变化得到的?
如图,它是由哪个基本图形经过怎样的变化得到的? 如图,在边长为5cm的正方形纸片ABCD中,点F在边BC上,已知FB=2cm.如果将纸折起,使点A落在点F上,则tan∠GEA=$\frac{5}{2}$.
如图,在边长为5cm的正方形纸片ABCD中,点F在边BC上,已知FB=2cm.如果将纸折起,使点A落在点F上,则tan∠GEA=$\frac{5}{2}$.