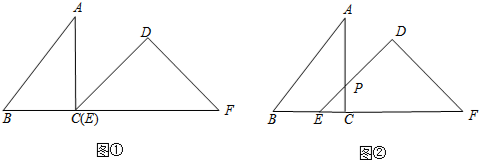题目内容
如图①是个长为2m,宽为n的长方形(m>n),沿图中虚线用剪刀分成四块小长方形,然后按图②的性状拼成一个正方形.

(1)图②中阴影部分的正方形的边长是多少?(用代数式表示)
(2)观察图②写出下列三个代数式:(m+n)2,(m-n)2,mn之间的等量关系.
(3)若m+n=7,mn=6,求m-n.

(1)图②中阴影部分的正方形的边长是多少?(用代数式表示)
(2)观察图②写出下列三个代数式:(m+n)2,(m-n)2,mn之间的等量关系.
(3)若m+n=7,mn=6,求m-n.
考点:列代数式,代数式求值
专题:
分析:(1)根据图形正方形的边长为是小长方形的长减去小长方形的宽(m-n)即可;
(2)(m+n)2,(m-n)2,mn分别表示的是大正方形、空白部分的正方形及小长方形的面积,利用大正方形的面积等于小正方形的面积加上4个小长方形的面积即可;
(3)整体代入(2)的变形得出答案即可.
(2)(m+n)2,(m-n)2,mn分别表示的是大正方形、空白部分的正方形及小长方形的面积,利用大正方形的面积等于小正方形的面积加上4个小长方形的面积即可;
(3)整体代入(2)的变形得出答案即可.
解答:解:(1)阴影部分的正方形的边长是(m+n);
(2)(m+n)2=(m-n)2+4mn;
(3)∵m+n=7,mn=6,
∴(m-n)2=(m+n)2-4mn=72-4×6=25
∴m-n=5.
(2)(m+n)2=(m-n)2+4mn;
(3)∵m+n=7,mn=6,
∴(m-n)2=(m+n)2-4mn=72-4×6=25
∴m-n=5.
点评:此题考查了对列代数式、代数式求值的理解与掌握.关键是通过观察图形,找出各图形之间的关系.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0). 如图,已知DE∥AB,DF∥AC,
如图,已知DE∥AB,DF∥AC, 如图,已知AB∥CD,∠B=40°,CN是∠BCE的平分线,CM⊥CN,求∠BCM的度数.
如图,已知AB∥CD,∠B=40°,CN是∠BCE的平分线,CM⊥CN,求∠BCM的度数. 如图所示,在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C为(-1,0),过点B作BD⊥x轴,垂足为D,且B点横坐标为-3.
如图所示,在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C为(-1,0),过点B作BD⊥x轴,垂足为D,且B点横坐标为-3. 已知,如图,O为?ABCD两条对角线的交点,AC=24mm,BD=38mm,BC=28mm,求△OAD的周长.
已知,如图,O为?ABCD两条对角线的交点,AC=24mm,BD=38mm,BC=28mm,求△OAD的周长.