题目内容
 如图,已知DE∥AB,DF∥AC,
如图,已知DE∥AB,DF∥AC,(1)试证∠A=∠EDF;
(2)利用平行线的性质,求∠A+∠B+∠C的度数.
考点:平行线的性质
专题:
分析:(1)先根据DE∥AB得出∠A=∠DEC,再由DF∥AE得出∠DEC=∠EDF,通过等量代换即可得出结论;
(2)根据DF∥AC,DE∥AB得出∠C=∠BDF,∠B=∠EDC.再由平角的定义得出∠BDF+∠EDF+∠EDC=180°,进而得出结论.
(2)根据DF∥AC,DE∥AB得出∠C=∠BDF,∠B=∠EDC.再由平角的定义得出∠BDF+∠EDF+∠EDC=180°,进而得出结论.
解答:(1)证明:∵DE∥AB,
∴∠A=∠DEC.
∵DF∥AE,
∴∠DEC=∠EDF,
∴∠A=∠EDF;
(2)证明:∵DF∥AC,DE∥AB,
∴∠C=∠BDF,∠B=∠EDC.
∵∠BDF+∠EDF+∠EDC=180°,
∴∠A+∠B+∠C=180°.
∴∠A=∠DEC.
∵DF∥AE,
∴∠DEC=∠EDF,
∴∠A=∠EDF;
(2)证明:∵DF∥AC,DE∥AB,
∴∠C=∠BDF,∠B=∠EDC.
∵∠BDF+∠EDF+∠EDC=180°,
∴∠A+∠B+∠C=180°.
点评:本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等,同旁内角互补是解答此题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,AD,BE是两条中线,若DE=3,则AB=( )
如图,在△ABC中,AD,BE是两条中线,若DE=3,则AB=( )| A、1 | B、3 | C、6 | D、9 |

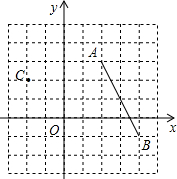 如图,在7×8网格中,每个小正方形的边长均为1,线段AB的端点和点C都在网格的格点上,以网格的两条格线建立直角坐标系,原点为0,A(2,3).
如图,在7×8网格中,每个小正方形的边长均为1,线段AB的端点和点C都在网格的格点上,以网格的两条格线建立直角坐标系,原点为0,A(2,3).