题目内容
20.计算:(1)(x+$\frac{x}{{x}^{2}-1}$)$÷(2+\frac{1}{x-1}-\frac{1}{x+1})$;
(2)-ax2-$\frac{1}{4}$a+ax;
(3)(x+3y)2+(2x+6y)(3y-4x)+(4x-3y)2.
分析 (1)利用平方差公式通分,再相除即可;
(2)先提取公因式,再运用完全平方公式求解即可;
(3)利用完全平方公式求解即可.
解答 解:(1)(x+$\frac{x}{{x}^{2}-1}$)$÷(2+\frac{1}{x-1}-\frac{1}{x+1})$
=$\frac{x(x+1)(x-1)+x}{(x+1)(x-1)}$÷$\frac{2(x+1)(x-1)+(x+1)-(x-1)}{(x+1)(x-1)}$,
=$\frac{{x}^{3}}{(x+1)(x-1)}$×$\frac{(x+1)(x-1)}{2{x}^{2}}$
=$\frac{x}{2}$;
(2)-ax2-$\frac{1}{4}$a+xa
=-a(x2-x+$\frac{1}{4}$)
=-a(x-$\frac{1}{2}$)2;
(3)(x+3y)2+(2x+6y)(3y-4x)+(4x-3y)2
=(x+3y)2+2(x+3y)(3y-4x)+(3y-4x)2
=(x+3y+3y-4x)2
=(6y-3x)2
=36y2-36xy+9x2.
点评 本题主要考查了分式的混合运算及整式的混合运算,解题的关键是熟记完全平方公式及平方差公式.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
10.下列计算正确的是( )
| A. | $\sqrt{{{(-6)}^2}}$=-6 | B. | -$\sqrt{{{(-6)}^2}}$=-6 | C. | $\sqrt{{{(-6)}^2}}$=±6 | D. | $\sqrt{6^2}$=±6 |
15.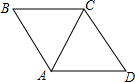 如图,△ABC与△ACD都是等边三角形,△ACD是由△ABC( )
如图,△ABC与△ACD都是等边三角形,△ACD是由△ABC( )
 如图,△ABC与△ACD都是等边三角形,△ACD是由△ABC( )
如图,△ABC与△ACD都是等边三角形,△ACD是由△ABC( )| A. | 绕点A顺时针旋转60°得到的 | B. | 绕点A顺时针旋转120°得到的 | ||
| C. | 绕点C顺时针旋转60°得到的 | D. | 绕点C顺时针旋转120°得到的 |
12.一个工人生产零件,计划30天完成,若每天多生产5个,则在26天里完成且多生产10个.若设原计划每天生产x个,则这个工人原计划每天生产多少个零件?根据题意可列方程( )
| A. | $\frac{30x-10}{x+5}$=26 | B. | $\frac{30x+10}{x+5}$=26 | C. | $\frac{30x}{x+5}$=26+10 | D. | $\frac{30x+10}{x-5}$=26 |
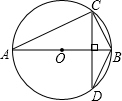 如右图,AB是⊙O的直径,CD是弦,且CD⊥AB,BC=6,AC=8,那么sin∠ABD的值是$\frac{4}{5}$.
如右图,AB是⊙O的直径,CD是弦,且CD⊥AB,BC=6,AC=8,那么sin∠ABD的值是$\frac{4}{5}$.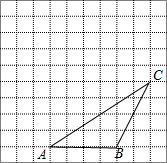 如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.
如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.