题目内容
8.在边长为4的正方形ABCD中,过点A的直线交边CD所在直线于点F,交对角线BD所在直线于点E.若DF=2,则BE=$\frac{8\sqrt{2}}{3}$或8$\sqrt{2}$.分析 分类讨论:当点F在DC上,如图1,利用正方形的性质得AB=CD=4,BD=4$\sqrt{2}$,AB∥CD,再证明△DEF∽△BEA,根据相似三角形的性质得$\frac{2}{4}$=$\frac{DE}{BE}$,则根据比例的性质可得BE=$\frac{2}{3}$BD=$\frac{8\sqrt{2}}{3}$;当点F在CD的延长线上时,如图2,同样可得$\frac{2}{4}$=$\frac{DE}{BE}$,则BD=DE,所以BE=2BD=8$\sqrt{2}$.
解答  解:当点F在DC上,如图1,
解:当点F在DC上,如图1,
∵四边形ABCD为正方形,
∴AB=CD=4,BD=4$\sqrt{2}$,AB∥CD,
∵DF∥AB,
∴△DEF∽△BEA,
∴$\frac{DF}{AB}$=$\frac{DE}{BE}$,即$\frac{2}{4}$=$\frac{DE}{BE}$,
∴$\frac{BE+DE}{BE}$=$\frac{3}{2}$,
∴BE=$\frac{2}{3}$BD=$\frac{8\sqrt{2}}{3}$; 当点F在CD的延长线上时,如图2,
当点F在CD的延长线上时,如图2,
∵DF∥AB,
∴△DEF∽△BEA,
∴$\frac{DF}{AB}$=$\frac{DE}{BE}$,即$\frac{2}{4}$=$\frac{DE}{BE}$,
∴BD=DE,
∴BE=2BD=8$\sqrt{2}$,
综上所述,BE的长为$\frac{8\sqrt{2}}{3}$或8$\sqrt{2}$.
故答案为$\frac{8\sqrt{2}}{3}$或8$\sqrt{2}$.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了正方形的性质和分类讨论思想的运用.

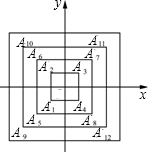 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,10,…,顶点A1,A2,A3,A4,A5,A6…的坐标分别为A1(-1,-1),A2(-1,1),A3(1,1),A4(1,-1),A5(-2,-2),A6(-2,2),…,则顶点A55的坐标是( )
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,10,…,顶点A1,A2,A3,A4,A5,A6…的坐标分别为A1(-1,-1),A2(-1,1),A3(1,1),A4(1,-1),A5(-2,-2),A6(-2,2),…,则顶点A55的坐标是( )| A. | (13,13) | B. | (-13,-13) | C. | (-14,-14) | D. | (14,14) |
| A. | y=4x+3 | B. | y=4x-3 | C. | y=4(x+3) | D. | y=4(x-3) |
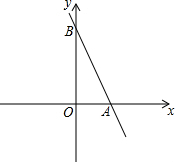 已知直线y=-2x+6与x轴交于点A,与y轴交于点B.
已知直线y=-2x+6与x轴交于点A,与y轴交于点B.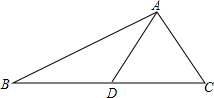 如图所示,在△ABC中,AD是BC边上的中线,且AD=$\frac{1}{2}$BC.
如图所示,在△ABC中,AD是BC边上的中线,且AD=$\frac{1}{2}$BC.