题目内容
1.阅读下列材料,然后回答问题.在进行二次根式的化简运算时,我们有时会碰上形如$\frac{2}{\sqrt{3}+1}$的式子,其实我们还可以将其进一步简化:$\frac{2}{\sqrt{3}+1}$=$\frac{2(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)}$=$\frac{2(\sqrt{3}-1)}{(\sqrt{3})^{2}-{1}^{2}}$=$\sqrt{3}$-1.以上这种化简的步骤叫做分母有理化.请用上面的方法化简:$\frac{1}{2-\sqrt{3}}$.
分析 仿照题中的方法将原式分母有理化即可.
解答 解:原式=$\frac{2+\sqrt{3}}{(2-\sqrt{3})(2+\sqrt{3})}$=2+$\sqrt{3}$.
点评 此题考查了分母有理化,熟练掌握分母有理化的方法是解本题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 如图,在?ABCD中,若点E、F分别是AB,CD的中点,连接AF,CE,DE,BF.DE与AF相交于点G,CE与BF相交于点H.求证:四边形GEHF是平行四边形.
如图,在?ABCD中,若点E、F分别是AB,CD的中点,连接AF,CE,DE,BF.DE与AF相交于点G,CE与BF相交于点H.求证:四边形GEHF是平行四边形. 如图,AD是△ABC的角平分线,点P在AD上,过点P作PE∥AB,PF∥AC,分别交BC于点E、F.
如图,AD是△ABC的角平分线,点P在AD上,过点P作PE∥AB,PF∥AC,分别交BC于点E、F.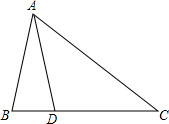 如图,在△ABC中,AB=AD=DC.
如图,在△ABC中,AB=AD=DC.