题目内容
13.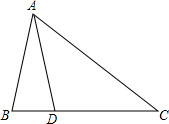 如图,在△ABC中,AB=AD=DC.
如图,在△ABC中,AB=AD=DC.(1)若∠BAD=30°,则∠B=75°,∠ADB=75°;
(2)若∠BAD=40°,求∠C的度数;
(3)若∠C=36°,求∠B的度数;
(4)若∠BAD=x,∠C=y,试用含x的式子表示y.
分析 (1)根据等腰三角形的性质及三角形内角和定理可求出∠B和∠ADB的度数;
(2)先根据等腰三角形的性质及三角形内角和定理可求出∠B的度数再根据三角形外角的性质可求出∠ADC的度数,再由三角形内角和定理解答即可.
(3)根据等腰三角形的性质及三角形外角的性质即可求得;
(4)根据等腰三角形的性质及三角形内角和定理可求出∠B的度数再根据三角形外角的性质可求出∠ADC的度数,再由三角形内角和定理解答即可.
解答 解:(1)∵AB=AD,∠BAD=30°,
∴∠B=∠ADB=$\frac{180-∠BAD}{2}$=$\frac{180°-30°}{2}$=75°,
故答案为75°,75°;
(2)∵AB=AD,∠BAD=40°,
∴∠B=$\frac{180-∠BAD}{2}$=$\frac{180°-40°}{2}$=70°,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=70°+40°=110°,
∵AD=DC,
∴∠C=$\frac{180°-∠ADC}{2}$=$\frac{180°-110°}{2}$=35°;
(3)∵AD=DC,
∴∠DAC=∠C=36°,
∵∠ADB是△ACD的外角,
∴∠ADB=2×36°=72°,
∵AB=AD,
∴∠B=∠ADB=72°;
(4)∵AB=AD,∠BAD=x,
∴∠B=$\frac{180-∠BAD}{2}$=$\frac{180°-x}{2}$,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=$\frac{180°-x}{2}$+x=90°+$\frac{1}{2}$x,
∵AD=DC,∠C=y,
∴y=$\frac{180°-∠ADC}{2}$=$\frac{1}{2}$(180°-90°-$\frac{1}{2}$x)=45°-$\frac{1}{4}$x.
点评 本题考查的是三角形内角和定理,三角形外角与外角性质以及等腰三角形的性质.此类题目考查学生分析各角之间关系的能力,运用所学的三角形知识点求解.

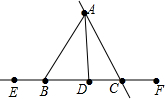 如图所示,图中能够写出的射线有9条,它们分别是射线AC,CA,EB,BE,BD,DB,DC,CD,FC;线段有13条,它们分别是线段AB,AD,AC,EB,ED,EC,EF,BC,BC,BF,DC,DF,CF.
如图所示,图中能够写出的射线有9条,它们分别是射线AC,CA,EB,BE,BD,DB,DC,CD,FC;线段有13条,它们分别是线段AB,AD,AC,EB,ED,EC,EF,BC,BC,BF,DC,DF,CF. Rt△ACB中,CD⊥AB于D,AF平分∠CAB交CD于E,交CB于F,过E作EG∥AB.若FG=1,BG=4,则EG的长为3.
Rt△ACB中,CD⊥AB于D,AF平分∠CAB交CD于E,交CB于F,过E作EG∥AB.若FG=1,BG=4,则EG的长为3.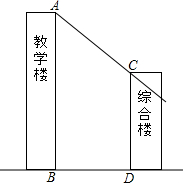 如图所示,综合楼高12m,两楼相距5m,在下午某一时刻太阳光与水平面的夹角为30°,当教学楼影子顶端A刚好落在综合楼顶端C处时,问教学楼的高度约为多少米?($\sqrt{3}$≈1.732,结果保留整数)
如图所示,综合楼高12m,两楼相距5m,在下午某一时刻太阳光与水平面的夹角为30°,当教学楼影子顶端A刚好落在综合楼顶端C处时,问教学楼的高度约为多少米?($\sqrt{3}$≈1.732,结果保留整数)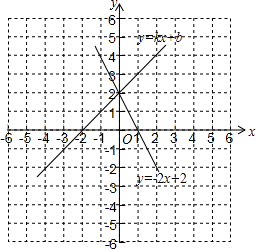 如图所示,平面直角坐标系中画出了一次函数y=-2x=2和一次函数y=kx+b的图象.
如图所示,平面直角坐标系中画出了一次函数y=-2x=2和一次函数y=kx+b的图象.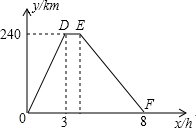 小王从A地前往B地送货,到达B地后,休息1h后按原路返回,他与A地的距离y(单位:km)和所用的时间x(单位;h)之间的函数关系式如图所示.
小王从A地前往B地送货,到达B地后,休息1h后按原路返回,他与A地的距离y(单位:km)和所用的时间x(单位;h)之间的函数关系式如图所示.