题目内容
6. 如图,AD是△ABC的角平分线,点P在AD上,过点P作PE∥AB,PF∥AC,分别交BC于点E、F.
如图,AD是△ABC的角平分线,点P在AD上,过点P作PE∥AB,PF∥AC,分别交BC于点E、F.(1)在图中画出线段PE和PF;
(2)点D到PE和PF的距离相等吗?请说明理由;
(3)当△ABC满足什么条件时,△PED≌△PFD(请填写一个合适的条件)?
分析 (1)根据平行线的画法画出线段PE和PF即可.
(2)首先由PE∥AB,PF∥AC,根据两直线平行,同位角相等,可得∠EPD=∠BAD,∠DPF=∠CAD,又由△ABC中,AD是它的角平分线,可得DP平分∠EPF,根据角平分线的性质,即可证得D到PE的距离与D到PF的距离相等;
(3)要确定添加的条件,首先要看现有的已知条件,∠EPD=∠FPD,还有一条公共边PD=PD,具备一角,一边分别对应相等,只要再任意一角能使得三角形全等,于是答案可得.
解答 (1)解:画出线段PE和PF如图所示:
(2)证明:∵PE∥AB,PF∥AC,
∴∠EPD=∠BAD,∠DPF=∠CAD,
∵△ABC中,AD是它的角平分线,
∴∠BAD=∠CAD,
∴∠EPD=∠DPF,
即PD平分∠EPF,
∴D到PE的距离与D到PF的距离相等;
(3)解:添加AB=AC,可根据等边对等角得出∠B=∠C,
∵PE∥AB,PF∥AC,
∴∠PED=∠B,∠PFD=∠C,
∴∠PED=∠PFD,
所以可根据AAS判定△PED≌△PFD.
点评 此题考查了角平分线的性质,平行线的性质以及三角形全等的判定.此题难度不大,解题的关键是熟记角平分线的性质定理的应用,注意数形结合思想的应用.

练习册系列答案
相关题目
17.已知抛物线的顶点坐标是P(1,3),且开口向下,下列说法正确的是( )
| A. | 当x≤1时,y随x的增大而减小 | B. | 当x≥1时,y随x的增大而增大 | ||
| C. | 当x<3时,y随x的增大而减小 | D. | 当x>3时,y随x的增大而减小 |
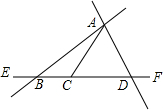 如图,能用字母表示的直线有3条,它们是直线AB,AD,EF;能用字母表示的线段有6条,它们是线段AB,AC,AD,BC,BD,CD;在直线EF上能用字母表示的射线有4条,它们是BC,CD,CB,DB.
如图,能用字母表示的直线有3条,它们是直线AB,AD,EF;能用字母表示的线段有6条,它们是线段AB,AC,AD,BC,BD,CD;在直线EF上能用字母表示的射线有4条,它们是BC,CD,CB,DB.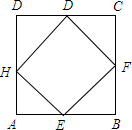 如图,长方形EFGH内接于边长为1的正方形ABCD,设AE=x,试求正方形EFGH的面积y与x的函数解析式,写出自变量x的取值范围,并求出AE=$\frac{1}{4}$时,正方形EFGH的面积.
如图,长方形EFGH内接于边长为1的正方形ABCD,设AE=x,试求正方形EFGH的面积y与x的函数解析式,写出自变量x的取值范围,并求出AE=$\frac{1}{4}$时,正方形EFGH的面积.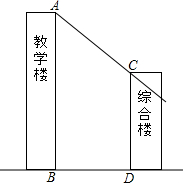 如图所示,综合楼高12m,两楼相距5m,在下午某一时刻太阳光与水平面的夹角为30°,当教学楼影子顶端A刚好落在综合楼顶端C处时,问教学楼的高度约为多少米?($\sqrt{3}$≈1.732,结果保留整数)
如图所示,综合楼高12m,两楼相距5m,在下午某一时刻太阳光与水平面的夹角为30°,当教学楼影子顶端A刚好落在综合楼顶端C处时,问教学楼的高度约为多少米?($\sqrt{3}$≈1.732,结果保留整数)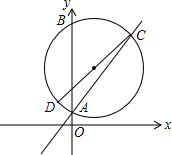 如图,半径为5的⊙O1,交直线y=x+2于A(0,2),C两点,交y轴与B(0,10),CD是⊙O1的直径,若函数y=$\frac{k}{x}$(x<0)的图象经过点D,求k的值.
如图,半径为5的⊙O1,交直线y=x+2于A(0,2),C两点,交y轴与B(0,10),CD是⊙O1的直径,若函数y=$\frac{k}{x}$(x<0)的图象经过点D,求k的值. 如图,在平面直角坐标系中,已知A(a,1),B(2,b),且a,b满足(2a-3b-2)2+$\sqrt{a-2b}$=0.
如图,在平面直角坐标系中,已知A(a,1),B(2,b),且a,b满足(2a-3b-2)2+$\sqrt{a-2b}$=0.