题目内容
7.不改变分式的值,将分式$\frac{{\frac{1}{2}x-\frac{2}{3}y}}{{\frac{1}{2}x+\frac{2}{3}y}}$的分子、分母的各项系数化为整数得$\frac{3x-4y}{3x+4y}$; 计算$\frac{m}{m-1}$+$\frac{1}{1-m}$的结果为1.分析 原式分子分母乘以6变形即可得到结果;原式变形后,利用同分母分式的减法法则计算即可得到结果.
解答 解:原式=$\frac{3x-4y}{3x+4y}$;原式=$\frac{m}{m-1}$-$\frac{1}{m-1}$=$\frac{m-1}{m-1}$=1.
故答案为:$\frac{3x-4y}{3x+4y}$;1.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.已知?ABCD中,∠B=4∠A,则∠D=( )
| A. | 18° | B. | 36° | C. | 72° | D. | 144° |
12.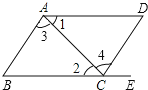 如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AD∥BE,且∠D=∠B;其中,能推出AB∥DC的条件为( )
如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AD∥BE,且∠D=∠B;其中,能推出AB∥DC的条件为( )
 如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AD∥BE,且∠D=∠B;其中,能推出AB∥DC的条件为( )
如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AD∥BE,且∠D=∠B;其中,能推出AB∥DC的条件为( )| A. | ①② | B. | ①③ | C. | ②③ | D. | 以上都错 |
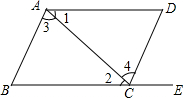 如图,给出下列条件:
如图,给出下列条件: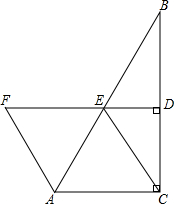 如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,且AF∥CE.
如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,且AF∥CE.