Question

16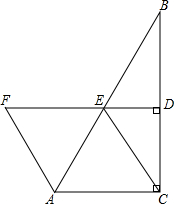．如图，在△ABC中，∠ACB=90°，BC的垂直平分线DE交BC于D，交AB于E，F在DE上，且AF∥CE．
（1）说明四边形ACEF是平行四边形；
（2）当∠B满足什么条件时，四边形ACEF是菱形，并说明理由．

Answer 1

分析 （1）易证∠DEC=∠DFA，即可得CE∥AF，根据CE=AF可得四边形ACEF为平行四边形；
（2）要使得平行四边形ACEF为菱形，则AC=CE，又CE=$\frac{1}{2}$AB，所以使得AB=2AC即可，根据AB、AC即可求得∠B的值．

解答 （1）证明：∵DE垂直平分BC，
∴∠EDB=90°，
∴DE∥AC，即FE∥AC，
∵AF∥CE，
∴四边形ACEF是平行四边形；

（2）当∠B=30°时，四边形ACEF是菱形．
理由：∵DE垂直平分BC，
∴BE=EC，
∴∠B=∠BCE，
∵∠B=30°，
∴∠BCE=30°，
∴∠AEC=∠B+∠BCE=30°+30°=60°．
∵∠BCA=90°∴∠BAC=90°-∠B=90°-30°=60°，
∴△ACE是等边三角形，
∴AC=EC．
∵四边形ACEF是平行四边形，
∴四边形ACEF是菱形．

点评 本题考查了平行四边形的判定，菱形的判定，垂直平分线的性质，本题中根据特殊角的正弦函数值求∠B的度数是解题的关键．