题目内容
17.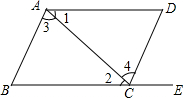 如图,给出下列条件:
如图,给出下列条件:①∠1=∠2;
②∠3=∠4;
③AD∥BE,且∠D=∠B;
④AD∥BE,且∠DCB=∠BAD;
其中能推出AB∥DC的条件为( )
| A. | ①② | B. | ②④ | C. | ②③ | D. | ②③④ |
分析 根据平行线的判定条件,逐一判断,排除错误答案.
解答 解:①∵∠1=∠2,∴AD∥BC,故此选项错误;
②∵∠3=∠4,∴AB∥DC,(内错角相等,两直线平行),故此选项正确;
③∵AD∥BC,∴∠B+∠BAD=180°,∵∠D=∠B,∴∠D+∠BAD=180°,由同旁内角互补,两直线平行可得AB∥DC,故此选项正确;
④∵AD∥BC,∴∠B+∠BAD=180°,∵∠BAD=∠BCD,∴∠B+∠BCD=180°,由同旁内角互补,两直线平行可得AB∥DC,故此选项正确;
故能推出AB∥DC的条件为:②③④.
故选D.
点评 此题考查了平行线的判定与性质,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
7.定义新运算:对于任意实数a,b,都有a⊕b=a2-3a+b,如3⊕5=32-3×3+5,若x⊕1=11,则实数x的值( )
| A. | 2或-5 | B. | -2或5 | C. | 2或5 | D. | -2或-5 |
8.若二次函数y=ax2+bx+c(a≠0)的图象上有两点,坐标分别为(x1,y1),(x2,y2),其中x1<x2,y1y2<0,则下列判断正确的是( )
| A. | a<0 | |
| B. | a>0 | |
| C. | 方程ax2+bx+c=0必有一根x0满足x1<x0<x2 | |
| D. | y1<y2 |
5. 将一副三角板(含30°、45°的直角三角形)摆放成如图所示,图中∠1的度数是( )
将一副三角板(含30°、45°的直角三角形)摆放成如图所示,图中∠1的度数是( )
 将一副三角板(含30°、45°的直角三角形)摆放成如图所示,图中∠1的度数是( )
将一副三角板(含30°、45°的直角三角形)摆放成如图所示,图中∠1的度数是( )| A. | 90° | B. | 120° | C. | 135° | D. | 150° |
9.下列事件中,属于必然事件的是( )
| A. | 抛一枚硬币,正面朝上 | |
| B. | 黑暗中从5把不同的钥匙中随意摸出一把,用它打开了门 | |
| C. | 打开电视机,任选一个频道,屏幕上正在播放新闻联播 | |
| D. | 4个人分成3组,其中一组必有2人 |
6.下列函数中,y随x增大而增大的一次函数是( )
| A. | y=-x-1 | B. | y=x-3 | C. | y=$\frac{3}{x}$ | D. | y=x2 |