题目内容
16.在平行四边形ABCD中,∠A:∠B=1:2,那么∠D=120°.分析 根据平行四边形的性质可知:∠D=∠B,又∠A+∠B=180°,∠A:∠B=1:2,即可求出∠D.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,∠D=∠B,
∴∠A+∠B=180,
∵∠A=$\frac{1}{2}$∠B,
∴3∠A=180°,
∴∠A=60°,
∴∠B=∠D=120°.
故答案为120°.
点评 本题考查平行四边形的性质,解题关键是熟练掌握平行四边形的性质,学会用方程思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
7.观察下列命题:
(1)如果a<0,b>0,那么a+b<0;
(2)直角都相等;
(3)同角的补角相等;
(4)如果两条直线被第三条直线所截,那么同位角相等.
其中真命题的个数是( )
(1)如果a<0,b>0,那么a+b<0;
(2)直角都相等;
(3)同角的补角相等;
(4)如果两条直线被第三条直线所截,那么同位角相等.
其中真命题的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
11.等腰三角形周长是24cm,一腰上的中线将周长分为15cm和9cm两部分,那么这个三角形的底边长是( )
| A. | 7.5cm | B. | 12cm | C. | 4cm | D. | 12cm或4cm |
1. 一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式bx+2k<0的解集是( )
一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式bx+2k<0的解集是( )
 一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式bx+2k<0的解集是( )
一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式bx+2k<0的解集是( )| A. | x<0 | B. | x<3 | C. | x>1 | D. | x<1 |
3. 如图,点A,B在线段EF上,点M,N分别是线段EA,BF的中点,EA:AB:BF=1:2:3,若MN=8cm,则线段EF的长是( )
如图,点A,B在线段EF上,点M,N分别是线段EA,BF的中点,EA:AB:BF=1:2:3,若MN=8cm,则线段EF的长是( )
 如图,点A,B在线段EF上,点M,N分别是线段EA,BF的中点,EA:AB:BF=1:2:3,若MN=8cm,则线段EF的长是( )
如图,点A,B在线段EF上,点M,N分别是线段EA,BF的中点,EA:AB:BF=1:2:3,若MN=8cm,则线段EF的长是( )| A. | 9cm | B. | 10cm | C. | 11cm | D. | 12cm |
3.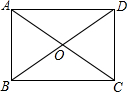 如图,已知四边形ABCD中,∠BAD=∠ABC=∠BCD=90°,下列条件能使四边形ABCD成为正方形的是( )
如图,已知四边形ABCD中,∠BAD=∠ABC=∠BCD=90°,下列条件能使四边形ABCD成为正方形的是( )
 如图,已知四边形ABCD中,∠BAD=∠ABC=∠BCD=90°,下列条件能使四边形ABCD成为正方形的是( )
如图,已知四边形ABCD中,∠BAD=∠ABC=∠BCD=90°,下列条件能使四边形ABCD成为正方形的是( )| A. | AC=BD | B. | AB⊥BC | C. | AD=BC | D. | AC⊥BD |
 如图,△ABC的三条中线为AD、BE、CF,在中线BE、CF上分别取点M、N,使BM=$\frac{1}{3}$BE,CN=$\frac{1}{3}$CF,求证:四边形EFMN是平行四边形.
如图,△ABC的三条中线为AD、BE、CF,在中线BE、CF上分别取点M、N,使BM=$\frac{1}{3}$BE,CN=$\frac{1}{3}$CF,求证:四边形EFMN是平行四边形.
 在长为10m,宽为8m的长方形空地上,沿平行于长方形各边的方向分割出三个形状、大小完全相同的小长方形花圃,其示意图如图所示.求出一个小长方形花圃的面积是8m2.
在长为10m,宽为8m的长方形空地上,沿平行于长方形各边的方向分割出三个形状、大小完全相同的小长方形花圃,其示意图如图所示.求出一个小长方形花圃的面积是8m2.