题目内容
3．
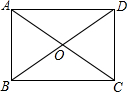如图，已知四边形ABCD中，∠BAD=∠ABC=∠BCD=90°，下列条件能使四边形ABCD成为正方形的是（ ）| A． | AC=BD | B． | AB⊥BC | C． | AD=BC | D． | AC⊥BD |
分析 根据已知条件可以判断四边形ABCD是矩形，则四条边相等的矩形是正方形或者对角线互相垂直的矩形是正方形．
解答 解：∵已知四边形ABCD中，∠BAD=∠ABC=∠BCD=90°，
∴四边形ABCD是矩形．
A、当AC=BD时，只能判定四边形ABCD是矩形，不能判定该矩形是正方形，故本选项错误；
B、矩形ABCD的四个角都是直角，则AB⊥BC，不能判定该矩形是正方形，故本选项错误；
C、矩形ABCD的对边AD=BC，不能判定该矩形是正方形，故本选项错误；
D、当矩形ABCD的对角线相互垂直，即AC⊥BD时，该矩形是正方形，故本选项正确；
故选：D．
点评 本题考查了正方形的判定．需要掌握矩形与正方形间的区别与联系．
练习册系列答案
阅读快车系列答案
相关题目
如图，在Rt△ABC中，∠B=90°，点D为AC的中点，以AB为一边向外作等边三角形ABE，连结DE．
沿圆柱体上底面直径截去一部分后的物体如右图所示，则它的俯视图是（ ）
18．某校在“6.26国际禁毒月”前组织七年级全体学生320人进行了一次“毒品预防知识”竞赛，赛后随机抽取了部分学生成绩进行统计，制作如下频数分布表和频数分布直方图，请根据图表提供的信息，解答下列问题
（1）表中a=12，b=0.2，并补全直方图
（2）若用扇形统计图描述此成绩分布情况，则分数段60≤x＜70对应扇形的圆心角度数是72°；
（3）请估计该年级分数在80≤x＜100的学生有多少人？
| 少分数段（x表示分数） | 频数 | 频率 |
| 50≤x＜60 60≤x＜70 70≤x＜80 | 4 8 A | 0.1 B 0.3 |
| 80≤x＜90 | 10 | 0.25 |
| 90≤x＜100 | 6 | 0.15 |
（1）表中a=12，b=0.2，并补全直方图
（2）若用扇形统计图描述此成绩分布情况，则分数段60≤x＜70对应扇形的圆心角度数是72°；
（3）请估计该年级分数在80≤x＜100的学生有多少人？
8．
直线${y_1}=-\frac{1}{2}x-\frac{5}{2}$与直线y2=2x在同一平面直角坐标系中的图象如图所示，则不等式y1≤y2的解集为（ ）
直线${y_1}=-\frac{1}{2}x-\frac{5}{2}$与直线y2=2x在同一平面直角坐标系中的图象如图所示，则不等式y1≤y2的解集为（ ）| A． | x≤-1 | B． | x≥-1 | C． | x≤-2 | D． | x≥-2 |
15．下列命题为假命题的是（ ）
| A． | 一角为36°的等腰三角形中必有一个角是72° | |
| B． | 等腰三角形两底角的平分线相等 | |
| C． | 有一个角等于60°的等腰三角形是等边三角形 | |
| D． | 等腰三角形底边上的高与顶角的角平分线重合 |
12．下列几何体中，主视图是矩形的是（ ）
| A． |  | B． |  | C． |  | D． |  |