题目内容
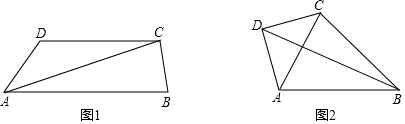
3．已知四边形的四条边长分别是a，b，c，d，其中a，b为对边，并且满足a2+b2+c2+d2=2ab+2cd，则这个四边形是（ ）| A． | 任意四边形 | B． | 平行四边形 | ||
| C． | 对角线相等的四边形 | D． | 对角线垂直的四边形 |
分析 把a2+b2+c2+d2=2ab+2cd变形得到a2-2ab+b2+c2-2cd+d2=0，则根据完全平方公式得到（a-b）2+（c-d）2=0，根据非负数的性质得a=b且c=d，然后根据平行四边形的判定方法求解．
解答 解：∵a2+b2+c2+d2=2ab+2cd，
∴a2-2ab+b2+c2-2cd+d2=0，
∴（a-b）2+（c-d）2=0，
∴a=b且c=d，
∵a，b为对边，
∵两组对边分别相等的四边形是平行四边形，
∴此四边形为平行四边形．
故选：B．
点评 本题考查了因式分解的运用：利用因式分解解决求值问题；利用因式分解解决证明问题；利用因式分解简化计算问题．也考查了非负数的性质和平行四边形的判定．
练习册系列答案
相关题目
如图，已知l1∥l2，直线l与l1、l2相交于C、D两点，把一块含30°角的三角尺按如图位置摆放．若∠1=130°，则∠2=20°．
如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法，其理由是同位角相等，两直线平行．
如图，斜坡AC的坡比为0.8：1，若BC=5，则斜坡AC=$\sqrt{41}$．