题目内容
如图，在?ABCD中，点E，F分别在BC，AD上，AE∥CF，请说明∠AFC与∠AEC的大小关系，并说明理由．考点：平行四边形的判定与性质
专题：
分析：平行四边形ABCD中，BC∥AD，可知∠DAE=∠AEB，又AE∥CF，可知∠DFC=∠DAE，继而得出∠DFC=∠AEB，从而得出结论．
解答：解：∠AFC=∠AEC，
理由如下：∵平行四边形ABCD中，BC∥AD，
又AE∥CF，
∴四边形AECF为平行四边形，
∴∠AEC=∠AFC．
理由如下：∵平行四边形ABCD中，BC∥AD，
又AE∥CF，
∴四边形AECF为平行四边形，
∴∠AEC=∠AFC．
点评：本题考查了平行四边形的性质，属于基础题，比较容易解答，注意熟练掌握平行四边形的性质是关键．
练习册系列答案
黄冈创优卷系列答案
相关题目
已知线段AB及AB上一点P，当点P满足下列哪一种关系时，点P为AB的黄金分割点：
①AP2=AB•PB；②AP=
AB；③PB=
AB；④
=
；⑤
=
．
其中正确的是（ ）
①AP2=AB•PB；②AP=
| ||
| 2 |
3-
| ||
| 2 |
| AP |
| PB |
| ||
| 2 |
| AB |
| AP |
| ||
| 2 |
其中正确的是（ ）
| A、①②③ | B、①②③④ |
| C、②③④⑤ | D、①②③④⑤ |
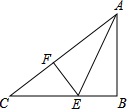如图，AE为∠BAC的平分线，EB⊥AB，EF⊥AC，则下列结论不正确的是（ ）| A、EF=EB |
| B、AF=AB |
| C、AE=CE |
| D、∠AEF=∠AEB |
如图，长方形内有两个相邻的正方形，面积分别为4和2，求阴影部分的面积．
如图，某拦河坝的横断面为梯形ABCD，若坝顶AD=3m，坝底BC=
如图，在⊙O中，直径AB⊥弦CD于点E．若BE=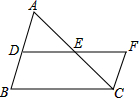
在△ABC中，点D，E分别是AB，AC的中点，连接DE并延长到点F，使EF=DE，连接CF．