题目内容
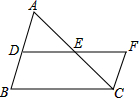 在△ABC中,点D,E分别是AB,AC的中点,连接DE并延长到点F,使EF=DE,连接CF.
在△ABC中,点D,E分别是AB,AC的中点,连接DE并延长到点F,使EF=DE,连接CF.(1)DE与BC有什么样的位置关系和数量关系?
(2)求证:四边形DBCF是平行四边形.
考点:三角形中位线定理,平行四边形的判定
专题:
分析:(1)根据三角形的中位线平行于第三边并且等于第三边的一半解答;
(2)利用一组对边平行且相等的四边形是平行四边形证明.
(2)利用一组对边平行且相等的四边形是平行四边形证明.
解答:(1)解:∵点D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE=
BC;
(2)证明:∵EF=DE,
∴DF=2DE,
∴DF∥BC且DF=BC,
∴四边形DBCF是平行四边形.
∴DE是△ABC的中位线,
∴DE∥BC,DE=
| 1 |
| 2 |
(2)证明:∵EF=DE,
∴DF=2DE,
∴DF∥BC且DF=BC,
∴四边形DBCF是平行四边形.
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半以及平行四边形的判定,熟记定理与平行四边形的判定方法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在?ABCD中,点E,F分别在BC,AD上,AE∥CF,请说明∠AFC与∠AEC的大小关系,并说明理由.
如图,在?ABCD中,点E,F分别在BC,AD上,AE∥CF,请说明∠AFC与∠AEC的大小关系,并说明理由.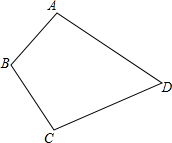 有四个汽车停车场,位于如图所示的四边形ABCD的四个顶点,现在要建立一个汽车维修站,你能利用“三角形任意两边之和大于第三边”,在四边形ABCD的内部找一点P,使点P到A,B,C,D四点的距离之和最小吗?
有四个汽车停车场,位于如图所示的四边形ABCD的四个顶点,现在要建立一个汽车维修站,你能利用“三角形任意两边之和大于第三边”,在四边形ABCD的内部找一点P,使点P到A,B,C,D四点的距离之和最小吗? 如图,在直线MN上找一点P,使点P到直线AB和直线CD的距离相等.
如图,在直线MN上找一点P,使点P到直线AB和直线CD的距离相等.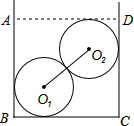 某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上,向内放入两个
某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上,向内放入两个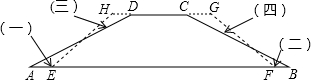
 如图,AB=DC,BF=CE,AE=DF,你能找到一对全等的三角形吗?说明理由.
如图,AB=DC,BF=CE,AE=DF,你能找到一对全等的三角形吗?说明理由.