题目内容
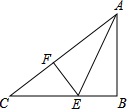 如图,AE为∠BAC的平分线,EB⊥AB,EF⊥AC,则下列结论不正确的是( )
如图,AE为∠BAC的平分线,EB⊥AB,EF⊥AC,则下列结论不正确的是( )| A、EF=EB |
| B、AF=AB |
| C、AE=CE |
| D、∠AEF=∠AEB |
考点:角平分线的性质
专题:
分析:根据角平分线上的点到角的两边距离相等可得EF=EB,再利用“HL”证明Rt△ABE和Rt△AFE全等,根据全等三角形对应边相等可得AF=AB,全等三角形对应角相等可得∠AEF=∠AEB.
解答:解:∵AE为∠BAC的平分线,EB⊥AB,EF⊥AC,
∴EF=EB,
在Rt△ABE和Rt△AFE中,
,
∴Rt△ABE≌Rt△AFE(HL),
∴AF=AB,∠AEF=∠AEB,
∴结论不正确的是AE=CE.
故选C.
∴EF=EB,
在Rt△ABE和Rt△AFE中,
|
∴Rt△ABE≌Rt△AFE(HL),
∴AF=AB,∠AEF=∠AEB,
∴结论不正确的是AE=CE.
故选C.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,熟记性质并求出全等三角形是解题的关键.

练习册系列答案
相关题目
 如图,下列推理错误的是( )
如图,下列推理错误的是( )| A、∵∠1=∠2,∴a∥b |
| B、∵∠1=∠3,∴a∥b |
| C、∵∠3=∠5,∴c∥d |
| D、∵∠2+∠4=180°,∴c∥d |
 如图,ACB是直线,AB⊥CD,EC⊥FC,图中共有( )对角互余.
如图,ACB是直线,AB⊥CD,EC⊥FC,图中共有( )对角互余.| A、2 | B、3 | C、4 | D、以上都不对 |
下列等式能够成立的是( )
A、(x-
| ||||
B、(x-
| ||||
C、(x-
| ||||
D、(x+
|
下列各对数中,互为相反数的是( )
A、
| ||||
B、
| ||||
| C、-1.75和+1.75 | ||||
| D、+2和-(-2) |
下列说法正确的是( )
| A、旋转后重合的两个图形成中心对称 |
| B、全等的两个图形一定成中心对称 |
| C、成中心对称的两个图形一定全等 |
| D、正三角形是中心对称图形 |
已知(x-y+3)2+
=0,则x+y的值为( )
| 2x+y |
| A、0 | B、-1 | C、1 | D、2 |
 如图,在?ABCD中,点E,F分别在BC,AD上,AE∥CF,请说明∠AFC与∠AEC的大小关系,并说明理由.
如图,在?ABCD中,点E,F分别在BC,AD上,AE∥CF,请说明∠AFC与∠AEC的大小关系,并说明理由.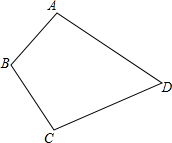 有四个汽车停车场,位于如图所示的四边形ABCD的四个顶点,现在要建立一个汽车维修站,你能利用“三角形任意两边之和大于第三边”,在四边形ABCD的内部找一点P,使点P到A,B,C,D四点的距离之和最小吗?
有四个汽车停车场,位于如图所示的四边形ABCD的四个顶点,现在要建立一个汽车维修站,你能利用“三角形任意两边之和大于第三边”,在四边形ABCD的内部找一点P,使点P到A,B,C,D四点的距离之和最小吗?